��Ŀ����
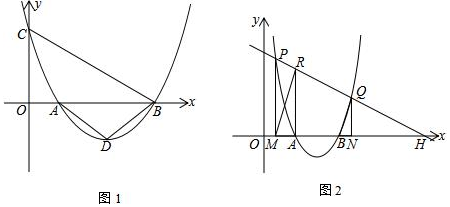
20����֪��OC�ǡ�AOB�ڲ���һ�����ߣ��ҡ�AOC=$\frac{1}{3}$��AOB����1����ͼ1��ʾ������AOB=120�㣬OMƽ�֡�AOB��ONƽ�֡�AOC�����MON�Ķ�����
��2����ͼ2��ʾ����AOB=x�㣬����OP������OQ�ֱ��OC��OB���������ֱ���ÿ��1���ÿ��2����ٶ����ŵ�O˳ʱ����ת��OP��OQ�ֱ�ֻ�ڡ�AOC�͡�BOC�ڲ���ת��
�ٵ��˶�t��ʱ����ֱ�д����AOP�͡�COQ�Ķ�������x��t��ʾ������AOP�͡�COQ��������ϵ��Σ�
������AOB=150�㣬��tΪ��ֵʱ��OP��OQ��
��3����ͼ3��ʾ����AOB��ֱ�ǣ���O�����������OD���ҡ�AOD-��BOD=��COD����ֱ��д����COD���AOB�Ķ���֮�ȣ�

���� ��1���ȸ�����֪�ã���AOC=40�㣬���ɽ�ƽ���ߵĶ���ͽǵĺͲ�ɵý��ۣ�
��2����ֱ�Ӹ����ٶȺ�ʱ���ʾ����COP=t��1=t�㣬��BOQ=t��2=2t�㣬����ɽǵĺ�����ʾ���ۣ��Ӷ��ɽ��ۿɵá�AOP�͡�COQ��������ϵ��
����ͼ��֪������COQ+��COP=90��ʱ��OP��OQ�����ݡ�COQ+��COP=90���е�ʽ�ɵý��ۣ�
��3���ȼ����AOC�Ķ���������֪��ʽ�ɵã���AOC=��BOD�����Եá�COD=30�㣬�ɵ����ıȵĹ�ϵ��
��� �⣺��1����ͼ1����OCƽ�֡�AOB��
���AOM=$\frac{1}{2}$��AOB=$\frac{1}{2}$��120��=60�㣬
�ߡ�AOC=$\frac{1}{3}$��AOB=$\frac{1}{3}$��120��=40�㣬
��ONƽ�֡�AOC��
���AON=$\frac{1}{2}$��AOC=20�㣬
���MON=��AOM-��AON=60��-20��=40�㣻
��2���١ߡ�AOC=$\frac{1}{3}$��AOB=$\frac{1}{3}x��$��
������ã���COP=t��1=t�㣬
��BOQ=t��2=2t�㣬
���AOP=��AOC-��COP=��$\frac{1}{3}x-t$���㣬
��COQ=��BOC-��BOQ=��$\frac{2}{3}x-2t$���㣬
���COQ=2��AOP��
�ڵ���COQ+��COP=90��ʱ��OP��OQ��
����$\frac{2}{3}$x-2t��+t=90��
��x=150����ã�$\frac{2}{3}$��150-2t+t=90��
t=10��
�൱t=10��ʱ��OP��OQ��
��3����ͼ3���ߡ�AOB=90�㣬��AOC=$\frac{1}{3}$��AOB��
���AOC=30�㣬
�ߡ�AOD-��BOD=��COD��
���AOC+��COD-��BOD=��COD��
���AOC=��BOD=30�㣬
���COD=90��-30��-30��=30�㣬
���COD����AOB=30�㣺90��=1��3��
���� �������йؽǵļ��㣬�����˽�ƽ���ߵĶ��塢��ֱ�Ķ����Լ��ǵĺͲ�֣�ע���������ν�ϵ�˼�룮

| A�� | 20=0 | B�� | a•2a=3a | C�� | ��ab2��3=3a3b6 | D�� | 2a6��a-2=2a8 |
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 5 |
| A�� | ��-6��-1�� | B�� | ��1��-6�� | C�� | ��6��1�� | D�� | ��6��-1�� |
| A�� | $\frac{x}{300}$=$\frac{2x+1.5}{300}$-93 | B�� | $\frac{x}{300}$=$\frac{2x+1.5}{300}$+93 | ||
| C�� | $\frac{x}{300}$=$\frac{2x+1.5}{300}$-$\frac{93}{3600}$ | D�� | $\frac{x}{300}$=$\frac{2x+1.5}{300}$+$\frac{93}{3600}$ |