题目内容
6.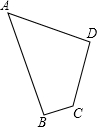 如图,四边形草坪ABCD中,∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m.
如图,四边形草坪ABCD中,∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m.(1)判断∠D是否是直角,并说明理由.
(2)求四边形草坪ABCD的面积.
分析 (1)连接AC,先根据勾股定理求出AC的长,再求出AD的长,结合勾股定理的逆定理得到∠D是直角;
(2)由S四边形ABCD=S△ABC+S△ADC即可得出结论.
解答 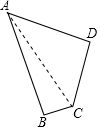 解:(1)∠D是直角,理由如下:
解:(1)∠D是直角,理由如下:
连接AC,
∵∠B=90°,AB=24m,BC=7m,
∴AC2=AB2+BC2=242+72=625,
∴AC=25(m).
又∵CD=15m,AD=20m,152+202=252,即AD2+DC2=AC2,
∴△ACD是直角三角形,或∠D是直角;
(2)S四边形ABCD=S△ABC+S△ADC
=$\frac{1}{2}$•AB•BC+$\frac{1}{2}$•AD•DC
=234(m2).
点评 本题考查的是勾股定理的应用,熟知勾股定理的应用是解答此题的关键.

练习册系列答案
相关题目
16.在△ABC中,三条边长分别为a,b,c,且a=n,b=$\frac{{n}^{2}}{4}$-1,c=$\frac{{n}^{2}}{4}$+1(n是大于2的偶数),求证:△ABC是直角三角形.
17.已知△ABC的三边a=m-n(m>n>0),b=m+n,c=2$\sqrt{mn}$.
(1)求证:△ABC是直角三角形;
(2)利用第(1)题的结论,写出两组m,n的值,要求三角形的边长均为整数.
(1)求证:△ABC是直角三角形;
(2)利用第(1)题的结论,写出两组m,n的值,要求三角形的边长均为整数.
14.已知2a>3b,则下列不等式中,正确的是( )
| A. | -8a>-12b | B. | 4a<6b | C. | 1-2a>1-3b | D. | 2a-1>3b-1 |
16.下列四个选项中,是同类项的一组是( )
| A. | -2x2y和-2x2 | B. | 3ab2与-3a2b | C. | 5a2与5b2 | D. | -πab2和2b2a |

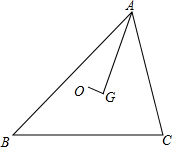 点O、G分别是△ABC的外心和重心,若AG⊥OG,求$\frac{A{B}^{2}+A{C}^{2}}{B{C}^{2}}$的值.
点O、G分别是△ABC的外心和重心,若AG⊥OG,求$\frac{A{B}^{2}+A{C}^{2}}{B{C}^{2}}$的值.