题目内容
3.用一正方形铁片剪一个直角边长分别为4cm和1cm的直角三角形铁片,所需正方形铁片的边长的最小值为$\frac{16}{5}$.分析 证明△AEF∽△DCE,得出 $\frac{AE}{DC}$=$\frac{EF}{CE}$=$\frac{1}{4}$,设AE=x,则AD=CD=4x,DE=AD-AE=3x,在Rt△CDE中,由勾股定理得出方程,解方程即可.
解答 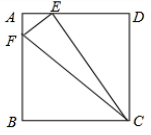 解:如图所示:
解:如图所示:
△CEF是直角三角形,∠CEF=90°,CE=4,EF=1,
∴∠AEF+∠CED=90°,
∵四边形ABCD是正方形,
∴∠A=∠D=90°,AD=CD,
∴∠DCE+∠CED=90°,
∴∠AEF=∠DCE,
∴△AEF∽△DCE,
∴$\frac{AE}{DC}$=$\frac{EF}{CE}$=$\frac{1}{4}$,
设AE=x,则AD=CD=4x,
∴DE=AD-AE=3x,
在Rt△CDE中,由勾股定理得:(3x)2+(4x)2=42,
解得:x=$\frac{4}{5}$,
∴AD=4×$\frac{4}{5}$=$\frac{16}{5}$;
故答案为:$\frac{16}{5}$.
点评 本题考查了勾股定理的应用.解题时,借用了相似三角形的判定与性质,难度较大.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
13.己知a是方程x2-3x-1=0的一个根,则代数式2a2-6a+3的值是( )
| A. | 6 | B. | 5 | C. | $12+2\sqrt{13}$ | D. | $12-2\sqrt{13}$ |
14.已知2a>3b,则下列不等式中,正确的是( )
| A. | -8a>-12b | B. | 4a<6b | C. | 1-2a>1-3b | D. | 2a-1>3b-1 |
12.要使方程x2-mx+m=-1有实数根,实数m的值可以是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 5 |
13.如果代数式$\frac{\sqrt{x}}{x-1}$有意义,那么x的取值范围是( )
| A. | x≥0且x≠1 | B. | x≠1 | C. | x>0 | D. | x≥0 |
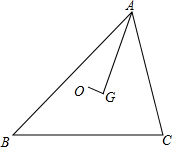 点O、G分别是△ABC的外心和重心,若AG⊥OG,求$\frac{A{B}^{2}+A{C}^{2}}{B{C}^{2}}$的值.
点O、G分别是△ABC的外心和重心,若AG⊥OG,求$\frac{A{B}^{2}+A{C}^{2}}{B{C}^{2}}$的值.