题目内容
如图，在△ABC中，CE，BF是两条高，若∠A=60°，求∠BOC的度数．考点：多边形内角与外角
专题：
分析：根据三角形内角和定理求得∠ABD=180°-60°-90°=30°．再有垂直的定义推知∠BEO=90°；最后又由三角形内角和定理来求∠BOC的度数；
解答：解：∵BD⊥AC，
∴∠BDA=90°．
又∵∠A+BDA+∠ABD=180°，
∴∠ABD=180°-60°-90°=30°．
又∵CE⊥AB，
∴∠BEO=90°，
∴∠BOC=∠ABD+∠BEO=30°+90°=120°．
∴∠BDA=90°．
又∵∠A+BDA+∠ABD=180°，
∴∠ABD=180°-60°-90°=30°．
又∵CE⊥AB，
∴∠BEO=90°，
∴∠BOC=∠ABD+∠BEO=30°+90°=120°．
点评：本题考查了三角形的角平分线、中线和高，三角形内角和定理．从三角形的一个顶点向底边作垂线，垂足与顶点之间的线段叫做三角形的高．
练习册系列答案
同步练习西南大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
如图，若正方形网格中每个小方格的边长为1，则△ABC是（ ）| A、直角三角形 |
| B、锐角三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
在①a4•a2②（-a2）3③a12÷a2④a2•a3⑤a3+a3中，计算结果为a6的个数是（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
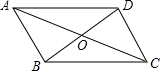如图，在?ABCD中，已知对角线AC、BD相交于点O．
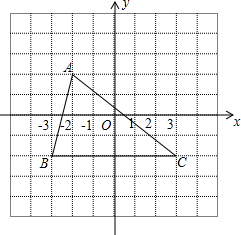如图，△ABC在直角坐标系中，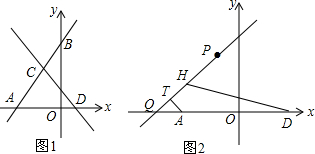
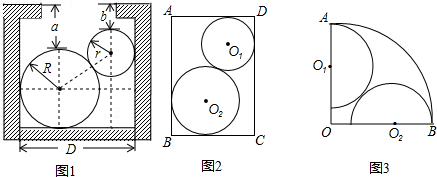
如图是一张铁片的示意图