题目内容
某铁路桥长1000m,现有一列火车从桥上通过,测得该火车从开始上桥到完全过桥共用了1min,整列火车完全在桥上的时间共40s.求火车的速度和长度.
(1)写出题目中的两个等量关系;
(2)给出上述问题的完整解答过程.
(1)写出题目中的两个等量关系;
(2)给出上述问题的完整解答过程.
考点:二元一次方程组的应用
专题:应用题
分析:(1)火车行驶速度×时间1分钟=桥长+火车长;火车行驶速度×40秒=桥长-火车长;
(2)根据(1)的等量关系,设出未知数,建立方程组即可.
(2)根据(1)的等量关系,设出未知数,建立方程组即可.
解答:解:(1)①火车行驶速度×时间1分钟=桥长+火车长;
②火车行驶速度×40秒=桥长-火车长.
(2)设火车的速度为xm/s,车长为ym,
由题意得:
,
解得:
.
答:火车的速度和车长分别为20米/秒和200米.
②火车行驶速度×40秒=桥长-火车长.
(2)设火车的速度为xm/s,车长为ym,
由题意得:
|
解得:
|
答:火车的速度和车长分别为20米/秒和200米.
点评:本题是一道行程问题,三个基本量:路程、速度、时间.关系式为:路程=速度×时间.题中的火车完全通过桥,实际告诉我们火车所行路程为桥长+火车长;整列火车在桥上实际告诉我们火车所行路程为桥长-火车长.

练习册系列答案
相关题目
某镇2012年投入教育经费2000万元,为了发展教育事业,该镇每年教育经费的年增长率均为x,预计到2014年共投入9500万元,则下列方程正确的是( )
| A、2000x2=9500 |
| B、2000(1+x)2=9500 |
| C、2000(1+x)=9500 |
| D、2000+2000(1+x)+2000(1+x)2=9500 |
 如图,AB∥CD,则∠1,∠2,∠3之间的关系是( )
如图,AB∥CD,则∠1,∠2,∠3之间的关系是( )| A、∠1+∠2+∠3=180° |
| B、∠1+∠2+∠3=360° |
| C、∠1+∠2-∠3=180° |
| D、∠1-∠2+∠3=180° |
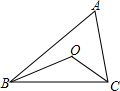 如图,在△ABC中,∠A=55°,AB、AC的垂直平分线交于点O,则∠BOC的度数为( )
如图,在△ABC中,∠A=55°,AB、AC的垂直平分线交于点O,则∠BOC的度数为( )| A、35° | B、60° |
| C、110° | D、150° |
 在直角△ABC纸片中,已知∠B=90°,AB=6,BC=8,折叠纸片使AB边与AC边重合,B点落在点E上,折痕为AD,则BD的长为( )
在直角△ABC纸片中,已知∠B=90°,AB=6,BC=8,折叠纸片使AB边与AC边重合,B点落在点E上,折痕为AD,则BD的长为( )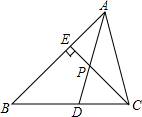 如图,已知AD是△ABC的角平分线,CE是△ABC的高,AD与CE相交于点P,∠BAC=66°,∠BCE=40°,求∠ADC和∠APC的度数.
如图,已知AD是△ABC的角平分线,CE是△ABC的高,AD与CE相交于点P,∠BAC=66°,∠BCE=40°,求∠ADC和∠APC的度数. 如图,在△ABC中,CE,BF是两条高,若∠A=60°,求∠BOC的度数.
如图,在△ABC中,CE,BF是两条高,若∠A=60°,求∠BOC的度数. 画图并填空:
画图并填空: