题目内容
在①a4•a2②（-a2）3③a12÷a2④a2•a3⑤a3+a3中，计算结果为a6的个数是（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
考点：同底数幂的除法,合并同类项,同底数幂的乘法,幂的乘方与积的乘方
专题：
分析：根据同底数幂的乘法，可判断①④，根据积的乘方，可判断②根据同底数幂的除法，可判断③，根据合并同类项，可判断⑤．
解答：解：①a4•a2=a4+2=a6，故①符合条件；
②（-a2）3=（-1）3a2×3=-a6，故②不符合条件；
③a12÷a2=a12-2=a10，故③不符合条件；
④a2•a3=a2+3=a5，故④不符合条件；
⑤a3+a3=2a3，故⑤不符合条件；
故选：A．
②（-a2）3=（-1）3a2×3=-a6，故②不符合条件；
③a12÷a2=a12-2=a10，故③不符合条件；
④a2•a3=a2+3=a5，故④不符合条件；
⑤a3+a3=2a3，故⑤不符合条件；
故选：A．
点评：本题考查了同底数幂的除法，底数不变指数相减．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
如图，两个完全相同的直角梯形重叠在一起，将其中一个直角梯形沿AD的方向平移，则阴影部分面积是下列从左到右的变形，是因式分解的是（ ）
| A、（a+3）（a-3）=a2-9 |
| B、x2+x-5=x（x+1）-5 |
| C、x2+4x+4=（x+2）2 |
| D、x2-4=（x-2）2 |
如图，AB∥CD，则∠1，∠2，∠3之间的关系是（ ）| A、∠1+∠2+∠3=180° |
| B、∠1+∠2+∠3=360° |
| C、∠1+∠2-∠3=180° |
| D、∠1-∠2+∠3=180° |
若a，b为实数，下列选项中真命题是（ ）
| A、若a＞b，则a2＞b2 | ||
B、若a=
| ||
| C、若|a|=|b|，则a=b | ||
| D、若a2＞b2，则a＞b |
在直角△ABC纸片中，已知∠B=90°，AB=6，BC=8，折叠纸片使AB边与AC边重合，B点落在点E上，折痕为AD，则BD的长为（ ）
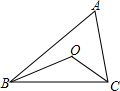如图，在△ABC中，∠A=55°，AB、AC的垂直平分线交于点O，则∠BOC的度数为（ ）| A、35° | B、60° |
| C、110° | D、150° |
如图，在△ABC中，CE，BF是两条高，若∠A=60°，求∠BOC的度数．