题目内容
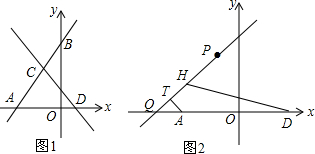
如图1所示,直线y=x+4分别交x轴、y轴于点A、B,直线y=kx-k交线段AB于点C,交x轴于点D,且S△ACD=5.
(1)求直线CD的解析式;
(2)直接写出不等式x+4>kx-k的解集 ;
(3)如图2所示,已知P(-1.5,2.5),Q为x轴上一动点,AT⊥PQ于T,且TH=AT,连接DH,当点Q运动时,∠DHP的大小是否变化?写出你的结论,并证明.
(1)求直线CD的解析式;
(2)直接写出不等式x+4>kx-k的解集
(3)如图2所示,已知P(-1.5,2.5),Q为x轴上一动点,AT⊥PQ于T,且TH=AT,连接DH,当点Q运动时,∠DHP的大小是否变化?写出你的结论,并证明.

考点:一次函数综合题
专题:压轴题
分析:(1)根据直线解析式求出点A的坐标,再求出点D的坐标,从而求出AD,联立两函数解析式求出点C的坐标,然后根据△ACD的面积列式求解得到k,即可得解;
(2)写出点C的坐标,再根据函数图象写出直线AB在直线CD上方部分的x的取值范围即可;
(3)连接PA、PD,利用勾股定理列式求出AP、PD,再求出AD,然后判断出△APD是等腰直角三角形,过点D作DM⊥PQ于M,利用同角的余角相等求出∠APT=∠PDM,再利用“角角边”求出△APT和△PDM全等,根据全等三角形对应边相等可得DM=PT,PM=AT,然后求出MH=DM,从而得到△MDH是等腰直角三角形,再根据等腰直角三角形的性质可得∠DHP=45°,值不变.
(2)写出点C的坐标,再根据函数图象写出直线AB在直线CD上方部分的x的取值范围即可;
(3)连接PA、PD,利用勾股定理列式求出AP、PD,再求出AD,然后判断出△APD是等腰直角三角形,过点D作DM⊥PQ于M,利用同角的余角相等求出∠APT=∠PDM,再利用“角角边”求出△APT和△PDM全等,根据全等三角形对应边相等可得DM=PT,PM=AT,然后求出MH=DM,从而得到△MDH是等腰直角三角形,再根据等腰直角三角形的性质可得∠DHP=45°,值不变.
解答:解:(1)令y=0,则x+4=0,
解得x=-4,
∴点A(-4,0),
令y=0,则kx-k=0,
解得x=1,
∴点D(1,0),
∴AD=1-(-4)=1+4=5,
联立
,
解得
,
∴S△ACD=
×5×
=5,
解得k=-
,
∴直线CD的解析式为y=-
x+
;
(2)∵k=-
,
∴
=-2,
=2,
∴点C的坐标为(-2,2),
∴不等式x+4>kx-k的解集x>-2;
故答案为:x>-2;
(3)如图,连接PA、PD,
∵A(-4,0),D(1,0),P(-1.5,2.5),
∴AP=
=
,
PD=
=
,
AD=5,
∵AP2+PD2=(
)2+(
)2=25=AD2,
∴△APD是等腰直角三角形,
过点D作DM⊥PQ于M,
则∠DPM+∠PDM=90°,∠APT+∠DPM=90°,
∴∠APT=∠PDM,
又∵AT⊥PQ,
∴∠ATP=∠PMD=90°,
在△APT和△PDM中,
,
∴△APT≌△PDM(AAS),
∴DM=PT,PM=AT,
∵TH=AT,
∴MH=PM+PH=AT+PH=TH+PH=PT=DM,
∴△MDH是等腰直角三角形,
∴∠DHP=45°,
故∠DHP的大小不变化.
解得x=-4,
∴点A(-4,0),
令y=0,则kx-k=0,
解得x=1,
∴点D(1,0),
∴AD=1-(-4)=1+4=5,
联立
|
解得
|
∴S△ACD=
| 1 |
| 2 |
| 5k |
| k-1 |
解得k=-
| 2 |
| 3 |
∴直线CD的解析式为y=-
| 2 |
| 3 |
| 2 |
| 3 |
(2)∵k=-
| 2 |
| 3 |
∴
| k+4 |
| k-1 |
| 5k |
| k-1 |
∴点C的坐标为(-2,2),
∴不等式x+4>kx-k的解集x>-2;
故答案为:x>-2;
(3)如图,连接PA、PD,
∵A(-4,0),D(1,0),P(-1.5,2.5),
∴AP=
| (-1.5+4)2+2.52 |
5
| ||
| 2 |
PD=
| (1+1.5)2+2.52 |
5
| ||
| 2 |
AD=5,
∵AP2+PD2=(
5
| ||
| 2 |
5
| ||
| 2 |
∴△APD是等腰直角三角形,

过点D作DM⊥PQ于M,
则∠DPM+∠PDM=90°,∠APT+∠DPM=90°,
∴∠APT=∠PDM,
又∵AT⊥PQ,
∴∠ATP=∠PMD=90°,
在△APT和△PDM中,
|
∴△APT≌△PDM(AAS),
∴DM=PT,PM=AT,
∵TH=AT,
∴MH=PM+PH=AT+PH=TH+PH=PT=DM,
∴△MDH是等腰直角三角形,
∴∠DHP=45°,
故∠DHP的大小不变化.
点评:本题是一次函数综合题型,主要考查了一次函数与坐标轴的交点问题,联立两函数解析式求交点坐标,三角形的面积,一次函数与不等式,等腰直角三角形的判定与性质,全等三角形的判定与性质,难点在于(3)作辅助线构造出全等三角形和等腰直角三角形并求出∠DHP是等腰直角三角形的锐角.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
下列从左到右的变形,是因式分解的是( )
| A、(a+3)(a-3)=a2-9 |
| B、x2+x-5=x(x+1)-5 |
| C、x2+4x+4=(x+2)2 |
| D、x2-4=(x-2)2 |
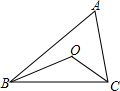 如图,在△ABC中,∠A=55°,AB、AC的垂直平分线交于点O,则∠BOC的度数为( )
如图,在△ABC中,∠A=55°,AB、AC的垂直平分线交于点O,则∠BOC的度数为( )| A、35° | B、60° |
| C、110° | D、150° |
 如图,在△ABC中,CE,BF是两条高,若∠A=60°,求∠BOC的度数.
如图,在△ABC中,CE,BF是两条高,若∠A=60°,求∠BOC的度数. 画图并填空:
画图并填空: 在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,点P从点A出发,沿折线ABCD方向以3cm/s的速度匀速运动;点Q从点D出发,沿线段DC方向以2cm/s的速度匀速运动.已知两点同时出发,当一个点到达终点时,另一点也停止运动,设运动时间为t(s).
在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,点P从点A出发,沿折线ABCD方向以3cm/s的速度匀速运动;点Q从点D出发,沿线段DC方向以2cm/s的速度匀速运动.已知两点同时出发,当一个点到达终点时,另一点也停止运动,设运动时间为t(s).