题目内容
5.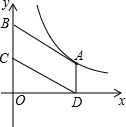 如图,在平面直角坐标系中,?ABCD的顶点A在函数y=$\frac{k}{x}(k>0,x>0)$的图象上,顶点B、C在y轴正半轴上(点B在点C的上方),若点D的坐标为(3,0),?ABCD的面积为4.5,则k的值为4.5.
如图,在平面直角坐标系中,?ABCD的顶点A在函数y=$\frac{k}{x}(k>0,x>0)$的图象上,顶点B、C在y轴正半轴上(点B在点C的上方),若点D的坐标为(3,0),?ABCD的面积为4.5,则k的值为4.5.
分析 设A(3,t),利用平行四边形的面积公式得到3t=4.5,可解得t=1.5,于是得到A点坐标,然后把A点坐标代入y=$\frac{k}{x}$中可计算出k的值.
解答 解:设A(3,t),
∵?ABCD的面积为4.5,
∴3t=4.5,解得t=1.5,
∴A点坐标为(3,1.5),
把A(3,1.5)代入y=$\frac{k}{x}$得k=3×1.5=4.5.
故答案为4.5.
点评 本题考查了反比例好图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了平行四边形的性质.

练习册系列答案
相关题目
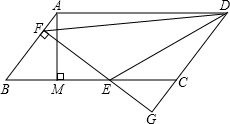 如图,平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上的一个动点(不与B、C重合).过E作直线AB的垂线,垂足为F.FE与DC的延长线相交于点G,当点E在线段BC上运动时,△BEF和△CEG的周长之和是不是定值?如果是定值,求出这个值;如果不是,请说明你的理由.
如图,平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上的一个动点(不与B、C重合).过E作直线AB的垂线,垂足为F.FE与DC的延长线相交于点G,当点E在线段BC上运动时,△BEF和△CEG的周长之和是不是定值?如果是定值,求出这个值;如果不是,请说明你的理由.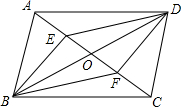 如图,已知四边形ABCD、EBFD均为平行四边形,AC、BD相交于点O,且A、E、O、F、C在同一条直线上,AC=8cm,AE=2cm,试求EF的长.
如图,已知四边形ABCD、EBFD均为平行四边形,AC、BD相交于点O,且A、E、O、F、C在同一条直线上,AC=8cm,AE=2cm,试求EF的长.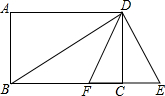 如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=4.设AB=x,AD=y,则x2+y2-8y的值为( )
如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=4.设AB=x,AD=y,则x2+y2-8y的值为( ) 已知矩形ABCD的两条对角线相交于O,∠AOD=120°,AD=3cm,求:
已知矩形ABCD的两条对角线相交于O,∠AOD=120°,AD=3cm,求: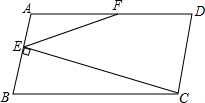 如图,?ABCD中,E为AB的中点,F为AD的中点,且CE⊥AB,若AB=4,CE=8,则EF的长为5.
如图,?ABCD中,E为AB的中点,F为AD的中点,且CE⊥AB,若AB=4,CE=8,则EF的长为5.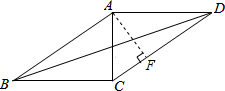 如图,已知四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,AF⊥CD,求AF的长度.
如图,已知四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,AF⊥CD,求AF的长度.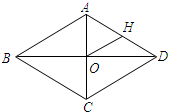 如图,在菱形ABCD中,对角线AC、BD相交于点O、H为边AD的中点,菱形的周长为48,则OH的长是6.
如图,在菱形ABCD中,对角线AC、BD相交于点O、H为边AD的中点,菱形的周长为48,则OH的长是6.