题目内容
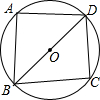 如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AB=AD,若BC+CD=6,则四边形ABCD的面积为( )
如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AB=AD,若BC+CD=6,则四边形ABCD的面积为( )| A、4 | B、9 | C、16 | D、25 |
考点:圆周角定理,勾股定理,等腰直角三角形
专题:
分析:由BD是⊙O的直径,AB=AD,可得△ADB为等腰直角三角形,则AD=
BD,根据三角形面积公式得S△ADB=
BD2,即BD2=4S△ADB,再利用完全平方公式,由BC+CD=6得BC2+CD2+2BC•CD=36,而BC2+CD2=BD2,S△DCB=
BC•CD,所以BD2+4S△DCB=36,易得4S△ADB+4S△DCB=36,于是可计算出S四边形ABCD=9.
| ||
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
解答:解:∵BD是⊙O的直径,AB=AD,
∴△ADB为等腰直角三角形,
∴由勾股定理可得:
AD=
BD,
∴S△ADB=
AD2=
BD2,
∴BD2=4S△ADB,
∵BC+CD=6,
∴BC2+CD2+2BC•CD=36,
∵BC2+CD2=BD2,S△DCB=
BC•CD,
∴BD2+4S△DCB=36,
即4S△ADB+4S△DCB=36,
∴S△ADB+S△DCB=9,
∴S四边形ABCD=S△ADB+S△DCB=9.
故选B.
∴△ADB为等腰直角三角形,
∴由勾股定理可得:
AD=
| ||
| 2 |
∴S△ADB=
| 1 |
| 2 |
| 1 |
| 4 |
∴BD2=4S△ADB,
∵BC+CD=6,
∴BC2+CD2+2BC•CD=36,
∵BC2+CD2=BD2,S△DCB=
| 1 |
| 2 |
∴BD2+4S△DCB=36,
即4S△ADB+4S△DCB=36,
∴S△ADB+S△DCB=9,
∴S四边形ABCD=S△ADB+S△DCB=9.
故选B.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了勾股定理和等腰直角三角形的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图是一个浅湖的平面图,图中所有曲线都表示湖与岸边的分界线,如果P点在岸上,那么A点和B点分别在( )
如图是一个浅湖的平面图,图中所有曲线都表示湖与岸边的分界线,如果P点在岸上,那么A点和B点分别在( )| A、点A在水中,点B在水中 |
| B、点A在水中,点B在岸上 |
| C、点A在岸上,点B在水中 |
| D、点A在岸上,点B在岸上 |
 如图,点E在BD上,AD=AE,AB=AC,∠1=∠2=20°,求∠CEA的度数.
如图,点E在BD上,AD=AE,AB=AC,∠1=∠2=20°,求∠CEA的度数.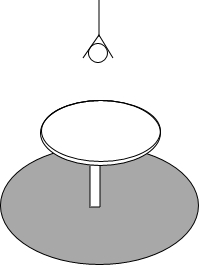 如图所示,直径为40cm的一张小圆桌桌面距离地面50cm,距离其正上方的一盏电灯的距离也是50cm
如图所示,直径为40cm的一张小圆桌桌面距离地面50cm,距离其正上方的一盏电灯的距离也是50cm 一个简单的起重机装置如图所示,其中AC=8m,AB=14m,∠BAC=60°.求BC的长.
一个简单的起重机装置如图所示,其中AC=8m,AB=14m,∠BAC=60°.求BC的长. 已知:如图,9×9的网格中(每个小正方形的边长为1)有一个格点△ABC.
已知:如图,9×9的网格中(每个小正方形的边长为1)有一个格点△ABC.