题目内容
 如图所示,AB是⊙O的一条直径,CD是⊙O的一条弦,延长BA与DC的延长线相交于P点,若AB=2PC,∠P=36°,求∠COD的度数.
如图所示,AB是⊙O的一条直径,CD是⊙O的一条弦,延长BA与DC的延长线相交于P点,若AB=2PC,∠P=36°,求∠COD的度数.考点:圆周角定理
专题:
分析:由AB=2PC,AB=2OC得到PC=OC,根据等腰三角形的性质得∠COP=∠P=36°,再利用三角形外角性质得到∠OCD=72°,由OC=OD,根据等腰三角形的性质及三角形内角和定理即可计算出∠COD.
解答:解:∵AB=2PC,AB=2OC,
∴PC=OC,
∴∠COP=∠P=36°,
∴∠OCD=∠COP+∠P=72°,
∵OC=OD,
∴∠ODC=∠OCD=72°,
∴∠COD=180°-∠ODC-∠OCD=36°.
∴PC=OC,
∴∠COP=∠P=36°,
∴∠OCD=∠COP+∠P=72°,
∵OC=OD,
∴∠ODC=∠OCD=72°,
∴∠COD=180°-∠ODC-∠OCD=36°.
点评:本题考查了圆周角定理,等腰三角形性质及三角形内角和定理,得出PC=OC是解题的关键.

练习册系列答案
相关题目
 如图,⊙O中,弦AB,CD相交于P点,连接AC,BD,则下列结论一定正确的是 ( )
如图,⊙O中,弦AB,CD相交于P点,连接AC,BD,则下列结论一定正确的是 ( )| A、∠A=∠B |
| B、∠C=∠D |
| C、PA:PB=PC:PD |
| D、PA:PD=PC:PB |
 一个简单的起重机装置如图所示,其中AC=8m,AB=14m,∠BAC=60°.求BC的长.
一个简单的起重机装置如图所示,其中AC=8m,AB=14m,∠BAC=60°.求BC的长. 已知:如图,9×9的网格中(每个小正方形的边长为1)有一个格点△ABC.
已知:如图,9×9的网格中(每个小正方形的边长为1)有一个格点△ABC. 如图,在四边形ABCD中,AD=12,DO=OB=5,AC=26,∠ADB=90°
如图,在四边形ABCD中,AD=12,DO=OB=5,AC=26,∠ADB=90°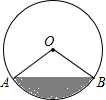 如图,有一个马戏帐篷,它的底部是圆形,其半径为20m,从a到b有一笔直的栅栏,其长为30m,观众在阴影区域里看马戏,如果每平方米可以坐三名观众,并且阴影区域坐满了人,那么大约有多少名观众在看马戏?
如图,有一个马戏帐篷,它的底部是圆形,其半径为20m,从a到b有一笔直的栅栏,其长为30m,观众在阴影区域里看马戏,如果每平方米可以坐三名观众,并且阴影区域坐满了人,那么大约有多少名观众在看马戏? 如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成了一个四边形,转动其中一张纸条,线段AD和BC的长度有什么关系?为什么?
如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成了一个四边形,转动其中一张纸条,线段AD和BC的长度有什么关系?为什么? 如图,
如图,