题目内容
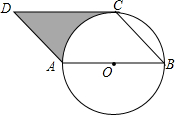 如图,已知在?ABCD中,AB=4,∠DAB=135°,以AB为直径的⊙O恰好经过点C.
如图,已知在?ABCD中,AB=4,∠DAB=135°,以AB为直径的⊙O恰好经过点C.(1)判断直线DC与⊙O的位置关系,并说明理由;
(2)求图中阴影部分的面积.(结果保留π)
考点:切线的判定,平行四边形的性质,扇形面积的计算
专题:计算题
分析:(1)连结OC,如图,根据平行四边形的性质得AD∥BC,CD∥AB,CD=AB=4,再根据平行线的性质可计算出∠B=180°-∠DAB=45°,由于OC=OB,则∠OCB=∠B=45°,所以∠BOC=90°,则∠OCD=90°,于是可根据切线的判定定理判断CD为⊙O的切线;
(2)根据梯形和扇形的面积公式,利用阴影部分的面积=S梯形AOCD-S扇形AOC进行计算即可.
(2)根据梯形和扇形的面积公式,利用阴影部分的面积=S梯形AOCD-S扇形AOC进行计算即可.
解答:解:(1)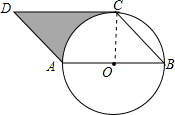 直线DC与⊙O相切.理由如下:
直线DC与⊙O相切.理由如下:
连结OC,如图,
∵四边形ABCD为平行四边形,
∴AD∥BC,CD∥AB,CD=AB=4,
∴∠DAB+∠B=180°,
∴∠B=180°-135°=45°,
∵OC=OB,
∴∠OCB=∠B=45°,
∴∠BOC=90°,
∴∠OCD=90°,
即OC⊥CD,
∴CD为⊙O的切线;
(2)阴影部分的面积=S梯形AOCD-S扇形AOC
=
(2+4)×2-
=6-π.
 直线DC与⊙O相切.理由如下:
直线DC与⊙O相切.理由如下:连结OC,如图,
∵四边形ABCD为平行四边形,
∴AD∥BC,CD∥AB,CD=AB=4,
∴∠DAB+∠B=180°,
∴∠B=180°-135°=45°,
∵OC=OB,
∴∠OCB=∠B=45°,
∴∠BOC=90°,
∴∠OCD=90°,
即OC⊥CD,
∴CD为⊙O的切线;
(2)阴影部分的面积=S梯形AOCD-S扇形AOC
=
| 1 |
| 2 |
| 90•π•22 |
| 360 |
=6-π.
点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了平行四边形的性质和扇形面积公式.

练习册系列答案
相关题目
下列事件中,必然事件是( )
| A、抛掷1个均匀的骰子,出现6点向上 |
| B、两直线被第三条直线所截,同位角相等 |
| C、366人中至少有2人的生日相同 |
| D、实数的绝对值是非负数 |
 如图,将甲图经过
如图,将甲图经过 在Rt△ABC中,∠C=90°,c=3,∠A=30°,求b和a的值.
在Rt△ABC中,∠C=90°,c=3,∠A=30°,求b和a的值.
 如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<12),连接DE,当△BDE是直角三角形时,t的值为
如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<12),连接DE,当△BDE是直角三角形时,t的值为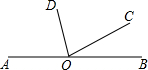 如图,∠BOC与∠AOC互为补角,OD平分∠AOC,∠BOC=n°,则∠DOB=
如图,∠BOC与∠AOC互为补角,OD平分∠AOC,∠BOC=n°,则∠DOB=