Question

7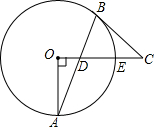．如图，⊙O中，半径OA⊥OE，弦AB交OE于D，过B作⊙O的切线，交OE的延长线于C，OA=3，BC=4，求AD的长．

Answer 1

分析 连结OB，如图，先根据切线的性质得到OB⊥BC，则利用勾股定理可计算出OC=5，接着证明∠CBD=∠CDB得到CD=CB=4，则OD=OC-CD=1，然后在Rt△OAD中利用勾股定理计算AD．

解答 解：连结OB，如图，
∵BC为切线，
∴OB⊥BC，
∴∠OBC=90°，
在Rt△OBC中，∵OB=3，BC=4，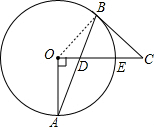
∴OC=$\sqrt{{3}^{2}+{4}^{2}}$=5，
∵OA⊥OC，OB⊥BC，
∴∠A+∠ODA=90°，∠OBA+∠CBD=90°，
而∠A=∠OBA，
∴∠ODA=∠CBD，
∵∠ODA=∠CDB，
∴∠CBD=∠CDB，
∴CD=CB=4，
∴OD=OC-CD=5-4=1，
在Rt△OAD中，AD=$\sqrt{O{D}^{2}+O{A}^{2}}$=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$．

点评 本题考查了切线的性质：圆的切线垂直于经过切点的半径．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．