题目内容
17.用正方形硬纸板做三棱柱盒子,每个盒子由3个长方形侧面和2个边长相同的三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用).A方法:剪6个侧面;
B方法:剪4个侧面和5个底面.
现有19张硬纸板,若裁剪出的侧面和底面恰好全部用完,求裁剪时几张用A方法,几张用B方法,并求出能做多少个盒子.

分析 设x张用A方法,y张用B方法,就可以分别表示出侧面个数和底面个数;再由侧面个数和底面个数比为3:2建立方程组,求出侧面的总数就可以求出结论.
解答 解:设裁剪时x张用A方法,y张用B方法.
由题意,得$\left\{\begin{array}{l}{x+y=19}\\{\frac{6x+4y}{5y}=\frac{3}{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=7}\\{y=12}\end{array}\right.$,
∴盒子的个数为:$\frac{6×7+4×12}{3}$=30.
答:裁剪时7张用A方法,12张用B方法,裁剪出的侧面和底面恰好全部用完,能做30个盒子.
点评 本题考查了二元一次方程组的应用,解答时根据裁剪出的侧面和底面个数相等建立方程组是关键.

练习册系列答案
相关题目
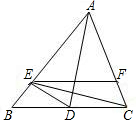 如图,AD是角平分线,E是AB上一点,AE=AC,EF∥BC交AC于F.下列结论①△ADC≌△ADE;②CE平分∠DEF;③AD垂直平分CE.其中正确的是①②③(填序号).
如图,AD是角平分线,E是AB上一点,AE=AC,EF∥BC交AC于F.下列结论①△ADC≌△ADE;②CE平分∠DEF;③AD垂直平分CE.其中正确的是①②③(填序号). 已知线段AB=m,CD=n,线段CD在直线AB上运动(A在B左侧,C在D左侧),若|m-2n|+$\sqrt{m+n-18}$=0.
已知线段AB=m,CD=n,线段CD在直线AB上运动(A在B左侧,C在D左侧),若|m-2n|+$\sqrt{m+n-18}$=0.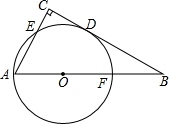 如图,在△ABC中,∠C=90°,以AB上的一点O为圆心.OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.
如图,在△ABC中,∠C=90°,以AB上的一点O为圆心.OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.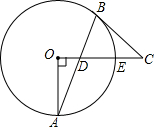 如图,⊙O中,半径OA⊥OE,弦AB交OE于D,过B作⊙O的切线,交OE的延长线于C,OA=3,BC=4,求AD的长.
如图,⊙O中,半径OA⊥OE,弦AB交OE于D,过B作⊙O的切线,交OE的延长线于C,OA=3,BC=4,求AD的长.