题目内容
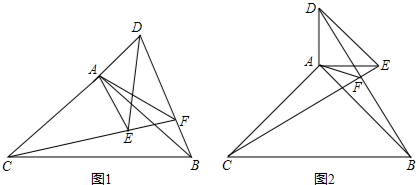
12.如图1,在△ABC和△ADE中,AC=AB,AE=AD,∠BAC=∠DAE=α,CE、DB交于点F,连接AF.(1)如图2,当α=90°时,猜想线段AF、BF、CF的数量关系,并证明你的结论;
(2)若AF=kBF,求$\frac{CF}{BF}$的值.(用含k、α的式子表示).
分析 (1)过点A作AP⊥AF交CE于点P,证出∠PAC=∠FAB,由∠BAC=∠DAE=90°得出∠CAE=∠BAD,由SAS证明△BAD≌△CAE,得出CE=BD,∠ACE=∠ABD,由ASA证明△ACP≌△ABF,得出AP=AF,△APF为等腰直角三角形,即可得出结论;
(2)过点A作AP⊥AF交CE于点P,可以得出△ABC∽△FBK,就有△KBC∽△FBA,根据等腰三角形的性质和三角函数即可得出结果.
解答 (1)解:猜想:CF=BF+$\sqrt{2}$AF,理由如下:
过点A作AP⊥AF交CE于点P,如图1所示:
∴∠BAC=∠PAF=90°,
∴∠BAC-∠PAO=∠PAF-∠PAH,
∴∠PAC=∠FAB,
∵∠BAC=∠DAE=90°
∴∠BAC+∠CAD=∠DAE+CAD,
即∠BAC=∠DAE,
在△BAD与△CAE中,
$\left\{\begin{array}{l}{AB=AC}&{\;}\\{∠BAD=∠CAE}&{\;}\\{AD=AE}&{\;}\end{array}\right.$,
∴△BAD≌△CAE(SAS).
∴BD=CE,∠ACE=∠ABD.
在△PAC和△FAB中,
$\left\{\begin{array}{l}{∠ACE=∠ABD}&{\;}\\{AC=AB}&{\;}\\{∠PAC=∠FAB}&{\;}\end{array}\right.$,
∴△PAC≌△FAB(ASA),
∴CP=BF,AP=AF,
∴△APF为等腰直角三角形
∴PF=$\sqrt{2}$AF,
∴CF=BF+$\sqrt{2}$AF;
(2)解:在CF上取FK=FB,连接BK,如图2所示:
∴∠FBK=∠FKB=$\frac{1}{2}$(180-∠BFK).
∵△BAD≌△CAE,
∴∠ACE=∠ABD,
∴∠CAB=∠BFK,
∵AC=AB,
∴∠ACB=∠ABC=$\frac{1}{2}$(180°-∠BAC),
∴∠ABC=∠FBK.
∴△ABC∽△FBK,
∴$\frac{AB}{BF}=\frac{BC}{BK}$,
∵∠ABC=∠FBK,
∴∠ABC-∠ABK=∠FBK-∠ABK,
∴∠KBC=∠FBA.
∴△KBC∽△FBA,
∴$\frac{KC}{FA}=\frac{KB}{BF}$,
∴CK=AF•$\frac{KB}{BF}$,
∵$\frac{\frac{1}{2}KB}{BF}=sin\frac{α}{2}$,
∴KB=2BF•sin$\frac{α}{2}$,
∴CK=AF•$\frac{2BF•sin\frac{α}{2}}{bf}$=AF•2sin$\frac{α}{2}$,
∴CF=BF+2AF•sin$\frac{α}{2}$,
∴$\frac{CF}{BF}$=$\frac{BF+2kBF•sin\frac{α}{2}}{bf}$=1+2ksin$\frac{α}{2}$.
点评 本题考查了全等三角形的判定及性质的运用,相似三角形的判定及性质的运用,锐角三角函数的运用,等腰三角形的性质的运用;解答时证明三角形全等是关键,证明三角形相似是难点.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案| A. | 24 | B. | 48 | C. | 10 | D. | 5 |
 如图所示,A,B,C三点在正方形网格线的交点处.若将△ACB绕着点A逆时针旋转到如图位置,得到△AC′B′,使A,C,B′三点共线,则旋转角为( )
如图所示,A,B,C三点在正方形网格线的交点处.若将△ACB绕着点A逆时针旋转到如图位置,得到△AC′B′,使A,C,B′三点共线,则旋转角为( )| A. | 30° | B. | 60° | C. | 20° | D. | 45° |
 已知线段AB=m,CD=n,线段CD在直线AB上运动(A在B左侧,C在D左侧),若|m-2n|+$\sqrt{m+n-18}$=0.
已知线段AB=m,CD=n,线段CD在直线AB上运动(A在B左侧,C在D左侧),若|m-2n|+$\sqrt{m+n-18}$=0. 如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B.直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q.
如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B.直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q.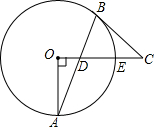 如图,⊙O中,半径OA⊥OE,弦AB交OE于D,过B作⊙O的切线,交OE的延长线于C,OA=3,BC=4,求AD的长.
如图,⊙O中,半径OA⊥OE,弦AB交OE于D,过B作⊙O的切线,交OE的延长线于C,OA=3,BC=4,求AD的长.