题目内容
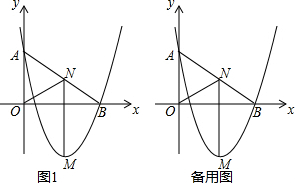
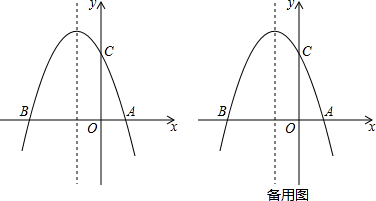
7.如图1,在平面直角坐标系中,O为坐标原点.直线y=kx+b与抛物线y=mx2-$\frac{19}{4}$x+n同时经过A(0,3)、B(4,0).(1)求m,n的值.
(2)点M是二次函数图象上一点,(点M在AB下方),过M作MN⊥x轴,与AB交于点N,与x轴交于点Q.求MN的最大值.
(3)在(2)的条件下,是否存在点N,使△AOB和△NOQ相似?若存在,求出N点坐标,不存在,说明理由.
分析 (1)根据抛物线y=mx2-$\frac{19}{4}$x+n经过A(0,3)、B(4,0),将两点坐标代入抛物线即可得出m,n的值;
(2)根据待定系数法可求经过AB两点的一次函数的解析式,得到MN=-$\frac{3}{4}$x+3-(x2-$\frac{19}{4}$x+3)=-x2+4x=-(x-2)2+4,从而求解;
(3)分两种情况讨论,①当ON⊥AB 时,②当N为AB中点时,依次求出点N的坐标即可.
解答 解:(1)∵抛物线y=mx2-$\frac{19}{4}$x+n经过A(0,3)、B(4,0),
∴$\left\{\begin{array}{l}{n=3}\\{16m-\frac{19}{4}×4+n=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=1}\\{n=3}\end{array}\right.$.
∴二次函数的表达式为y=x2-$\frac{19}{4}$x+3.
(2)∵直线y=kx+b经过A(0,3)、B(4,0),则$\left\{\begin{array}{l}{b=3}\\{4k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=3}\end{array}\right.$.
∴经过AB两点的一次函数的解析式为y=-$\frac{3}{4}$x+3.
MN=-$\frac{3}{4}$x+3-(x2-$\frac{19}{4}$x+3)=-x2+4x=-(x-2)2+4,
∵0≤x≤4,
∴当x=2时,MN取得最大值为4.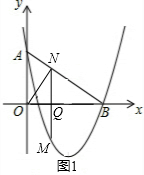 (3)存在.
(3)存在.
①当ON⊥AB时,(如图1)
可证:∠NOQ=∠OAB,∠OQN=∠AOB=90°,
∴△AOB∽△OQN.
∴$\frac{ON}{AB}$=$\frac{NQ}{OB}$=$\frac{OQ}{OA}$,
∴OA=3,OB=4,
∴AB=5,
∵ON•AB=OA•OB,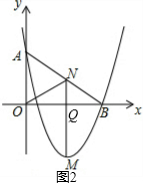 ∴ON=$\frac{12}{5}$,
∴ON=$\frac{12}{5}$,
∴NQ=$\frac{36}{25}$,OQ=$\frac{48}{25}$.
∴N($\frac{36}{25}$,$\frac{48}{25}$);
②当N为AB中点时,(如图2)
∠NOQ=∠B,∠AOB=∠NQO=90°,
∴△AOB∽∽△NQO.此时N(2,$\frac{3}{2}$).
∴满足条件的N($\frac{36}{25}$,$\frac{48}{25}$)或N(2,$\frac{3}{2}$).
点评 本题考查了二次函数综合题,涉及了待定系数法求函数解析式、配方法及相似三角形的判定,综合考察的知识点较多,像此类综合题,要求同学们一步一步的来,找准突破口,将所学的知识融会贯通.

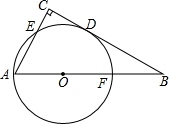 如图,在△ABC中,∠C=90°,以AB上的一点O为圆心.OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.
如图,在△ABC中,∠C=90°,以AB上的一点O为圆心.OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.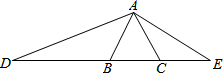 如图,△ABC是等边三角形,D为CB延长线上一点,E为BC延长线上点,且∠DAE=120°
如图,△ABC是等边三角形,D为CB延长线上一点,E为BC延长线上点,且∠DAE=120°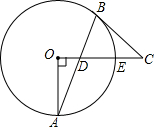 如图,⊙O中,半径OA⊥OE,弦AB交OE于D,过B作⊙O的切线,交OE的延长线于C,OA=3,BC=4,求AD的长.
如图,⊙O中,半径OA⊥OE,弦AB交OE于D,过B作⊙O的切线,交OE的延长线于C,OA=3,BC=4,求AD的长.
 如图,将三角形ABC先向左平移5个单位长度,再向下平移4个单位长度得到三角形A1B1C1.
如图,将三角形ABC先向左平移5个单位长度,再向下平移4个单位长度得到三角形A1B1C1.