题目内容
4.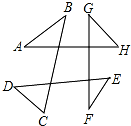 如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数为( )
如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数为( )| A. | 90° | B. | 180° | C. | 270° | D. | 360° |
分析 根据三角形的外角等于不相邻的两个内角的和,以及多边形的内角和即可求解.
解答  解:∵∠1=∠A+∠B,∠2=∠C+∠D,∠3=∠E+∠F,∠4=∠G+∠H,
解:∵∠1=∠A+∠B,∠2=∠C+∠D,∠3=∠E+∠F,∠4=∠G+∠H,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=∠1+∠2+∠3+∠4,
又∵∠1+∠2+∠3+∠4=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=360°.
故选D.
点评 本题考查了三角形的外角的性质以及多边形的外角和定理,正确转化为多边形的外角和是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
15.矩形具有而平行四边形不具有的性质是( )
| A. | 对角线互相平分 | B. | 对角线相等 | C. | 对角线互相垂直 | D. | 四边相等 |
12.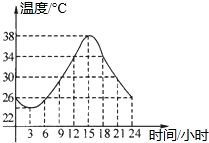 如图所示是某市夏天的温度随时间变化的图象,通过观察可知,下列说法中错误的是( )
如图所示是某市夏天的温度随时间变化的图象,通过观察可知,下列说法中错误的是( )
 如图所示是某市夏天的温度随时间变化的图象,通过观察可知,下列说法中错误的是( )
如图所示是某市夏天的温度随时间变化的图象,通过观察可知,下列说法中错误的是( )| A. | 这天15时温度最高 | |
| B. | 这天3时温度最低 | |
| C. | 这天最高温度与最低温度的差是13℃ | |
| D. | 这天0-3时,15-24时温度在下降 |
19.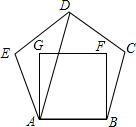 把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG=( )
把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG=( )
 把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG=( )
把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG=( )| A. | 18° | B. | 20° | C. | 28° | D. | 30° |
16.计算-2+1的结果是( )
| A. | -3 | B. | -1 | C. | 3 | D. | 1 |
 已知:如图,在平行四边形ABCD中,E,F分别是AB,CD上的两点,且AE=CF,AF、DE相交于点N,BF、CE相交于点M.求证:四边形EMFN是平行四边形.
已知:如图,在平行四边形ABCD中,E,F分别是AB,CD上的两点,且AE=CF,AF、DE相交于点N,BF、CE相交于点M.求证:四边形EMFN是平行四边形.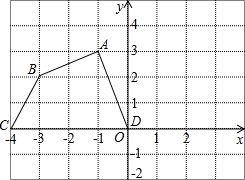 如图,在平面直角坐标系中,四边形ABCD各个顶点的坐标分别为A(-1,3),B(-3,2),C(-4,0),D(0,0)
如图,在平面直角坐标系中,四边形ABCD各个顶点的坐标分别为A(-1,3),B(-3,2),C(-4,0),D(0,0)