题目内容
7.如图方格纸中每个小正方形的边长均为1,点A,B在小正方形的顶点上.(1)在图1中画出等腰钝角△ABC(点C在小正方形的顶点上),使△ABC的面积为2;
(2)在图2中画出等腰直角△ABC(点C在小正方形的顶点上),使∠ABC=90°.
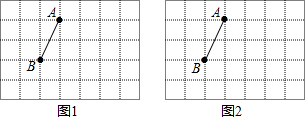
分析 (1)直接利用等腰三角形的性质结合三角形的面积求法得出即可;
(2)直接利用等腰三角形的性质结合直角三角形的性质得出即可.
解答 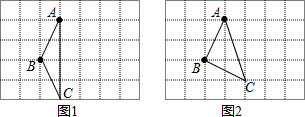 解:(1)如图1所示:△ABC即为所求;
解:(1)如图1所示:△ABC即为所求;
(2)如图2所示:△ABC即为所求.
点评 此题主要考查了应用设计与作图,正确利用等腰三角形的性质得出是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.矩形具有而平行四边形不具有的性质是( )
| A. | 对角线互相平分 | B. | 对角线相等 | C. | 对角线互相垂直 | D. | 四边相等 |
2.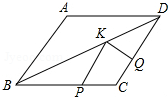 如图,在菱形ABCD中,AB=4,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
如图,在菱形ABCD中,AB=4,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
 如图,在菱形ABCD中,AB=4,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
如图,在菱形ABCD中,AB=4,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 2$\sqrt{3}$+2 |
12.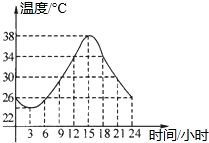 如图所示是某市夏天的温度随时间变化的图象,通过观察可知,下列说法中错误的是( )
如图所示是某市夏天的温度随时间变化的图象,通过观察可知,下列说法中错误的是( )
 如图所示是某市夏天的温度随时间变化的图象,通过观察可知,下列说法中错误的是( )
如图所示是某市夏天的温度随时间变化的图象,通过观察可知,下列说法中错误的是( )| A. | 这天15时温度最高 | |
| B. | 这天3时温度最低 | |
| C. | 这天最高温度与最低温度的差是13℃ | |
| D. | 这天0-3时,15-24时温度在下降 |
19.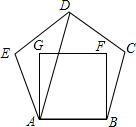 把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG=( )
把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG=( )
 把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG=( )
把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG=( )| A. | 18° | B. | 20° | C. | 28° | D. | 30° |
16.计算-2+1的结果是( )
| A. | -3 | B. | -1 | C. | 3 | D. | 1 |
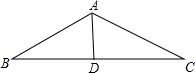 如图,在△ABC中,AB=17,BC=30,BC边上的中线AD=8,∠B与∠C相等吗?
如图,在△ABC中,AB=17,BC=30,BC边上的中线AD=8,∠B与∠C相等吗?