题目内容
2.如图1,正方形ABCD中,点A在双曲线y=$\frac{k}{x}$(x>0)上,点C、D在y轴上,已知点B(2,3).(1)求k值;
(2)在①的基础上,将正方形ABCD平移,使点A、C恰好落在此双曲线y=$\frac{k}{x}$(x>0)上,如图2,求此时点B的坐标.
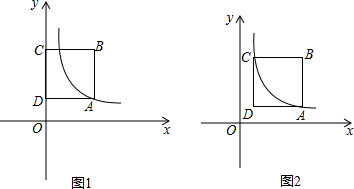
分析 (1)根据正方形的性质求得A的坐标,然后根据待定系数法求得即可;
(2)把y=3代入(1)求得的解析式即可求得C的坐标,然后根据正方形的性质即可求得B的坐标.
解答 解:(1)∵四边形ABCD是正方形,B(2,3),
∴AB=BC=CD=DA=2,
∴A(2,1),
代入y=$\frac{k}{x}$(x>0)得1=$\frac{k}{2}$,
解得k=2;
(2)∵C的纵坐标为3,
把y=3代入y=$\frac{2}{x}$得3=$\frac{2}{x}$,
解得x=$\frac{2}{3}$,
∵AB=BC=CD=DA=2,
∴B($\frac{8}{3}$,3).
点评 本题考查了反比例函数图象上点的坐标特征和正方形的性质,(2)求得C的坐标是解题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
14.下列计算正确的是( )
| A. | a+2a=3a2 | B. | (ab2)3=a3b6 | C. | (am)2=am+2 | D. | a3•a2=a6 |
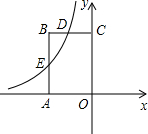 如图,矩形OABC的顶点A,C分别在x轴和y轴上,若OA=4,OC=6,写出一个函数y=$\frac{k}{x}({k≠0})$,使它的图象与矩形OABC的两边AB,BC分别交于点D,E,这个函数的表达式为y=-$\frac{1}{x}$.
如图,矩形OABC的顶点A,C分别在x轴和y轴上,若OA=4,OC=6,写出一个函数y=$\frac{k}{x}({k≠0})$,使它的图象与矩形OABC的两边AB,BC分别交于点D,E,这个函数的表达式为y=-$\frac{1}{x}$.
 如图,AB半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则tanα的值为$\frac{3}{2}$.
如图,AB半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则tanα的值为$\frac{3}{2}$.