题目内容
12.已知一次函数y=(1-2m)x+m-1,求满足下列条件的m的值.(1)函数值y随x的增大而增大;
(2)函数图象与y轴的负半轴相交;
(3)函数的图象过二、三、四象限;
(4)函数的图象过原点.
分析 利用一次函数的性质得到有关m的不等式(组)或方程求解即可.
解答 解:(1)∵函数值y随x的增大而增大,
∴1-2m>0,
解得:m<$\frac{1}{2}$,
∴当m<$\frac{1}{2}$时,函数值y随x的增大而增大;
(2)∵函数图象与y轴的负半轴相交,
∴m-1<0,
解得:m<1,
∴当m<1时,函数图象与y轴的负半轴相交;
(3)∵函数的图象过二、三、四象限,
∴$\left\{\begin{array}{l}{1-2m<0}\\{m-1<0}\end{array}\right.$,
解得:$\frac{1}{2}$<m<1,
∴当$\frac{1}{2}$<m<1时,函数的图象过二、三、四象限;
(4)∵函数图象过原点,
∴m-1=0,
解得:m=1,
∴当m=1时,函数图象过原点.
点评 本题主要考查一次函数图象在坐标平面内的位置与k、b的关系.解答本题注意理解:直线y=kx+b所在的位置与k、b的符号有直接的关系.k>0时,直线必经过一、三象限;k<0时,直线必经过二、四象限;b>0时,直线与y轴正半轴相交;b=0时,直线过原点;b<0时,直线与y轴负半轴相交.

练习册系列答案
相关题目
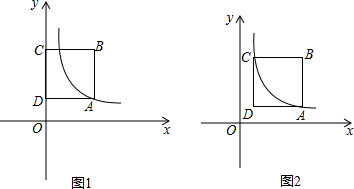
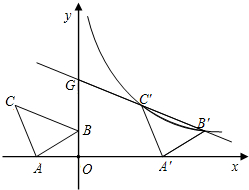 如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,d)、C(-3,2).
如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,d)、C(-3,2).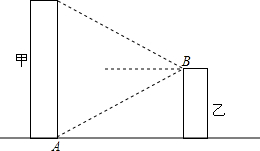 某城市搞亮化工程,如图,在甲楼底部,乙楼顶部分别安装一盏射灯.已知A灯恰好照到B灯,B灯恰好照到甲楼的顶部,如果两盏灯的光线与水平线的夹角相等,那么能否说甲楼的高度是乙楼的2倍?说说你的看法.
某城市搞亮化工程,如图,在甲楼底部,乙楼顶部分别安装一盏射灯.已知A灯恰好照到B灯,B灯恰好照到甲楼的顶部,如果两盏灯的光线与水平线的夹角相等,那么能否说甲楼的高度是乙楼的2倍?说说你的看法.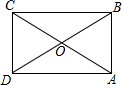 如图,在矩形ABCD中,对角线AC、BD相交于点O,OA=AB,OD=3cm,则矩形ABCD的面积为9$\sqrt{3}$cm2.
如图,在矩形ABCD中,对角线AC、BD相交于点O,OA=AB,OD=3cm,则矩形ABCD的面积为9$\sqrt{3}$cm2. 在长为30m,宽为20m的草地上造两条宽均为1m互相垂直的小道(如图),则剩余草地面积为551m2.
在长为30m,宽为20m的草地上造两条宽均为1m互相垂直的小道(如图),则剩余草地面积为551m2.