题目内容
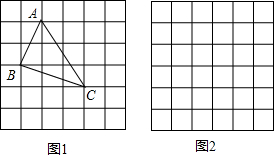
19.问题背景:在△ABC中,AB、BC、AC三边的长分别为$\sqrt{5}$、$\sqrt{10}$、$\sqrt{13}$,求此三角形的面积.小军同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示,这样不需要求△ABC的高,而借用网格就能计算它的面积.
(1)请将△ABC的面积直接填写在横线上:$\frac{7}{2}$.
(2)我们把上述求△ABC面积的方法叫做构图法,如果△ABCD的三边长分别为$\sqrt{5}$a,$\sqrt{13}$a,2$\sqrt{5}$a,请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
(3)若△ABC三边的长分别为$\sqrt{9{m}^{2}+4{n}^{2}}$、$\sqrt{{m}^{2}+4{n}^{2}}$、2$\sqrt{{m}^{2}+4{n}^{2}}$(m>0,n>0,且m≠n),试运用构图法画出相应的△ABC,并求出这个三角形的面积.
分析 (1)△ABC的面积=正方形面积减去三个三角形面积,求出即可;
(2)$\sqrt{5}$a是直角边长为a,2a的直角三角形的斜边;2$\sqrt{2}$a是直角边长为2a,2a的直角三角形的斜边;$\sqrt{17}$a是直角边长为a,4a的直角三角形的斜边,把它整理为一个矩形的面积减去三个直角三角形的面积;
(3)结合(1),(2)易得此三角形的三边分别是直角边长为m,4n的直角三角形的斜边;直角边长为3m,2n的直角三角形的斜边;直角边长为2m,2n的直角三角形的斜边.同样把它整理为一个矩形的面积减去三个直角三角形的面积.
解答 解:(1)根据题意得:S△ABC=32-$\frac{1}{2}$×1×2-$\frac{1}{2}$×2×3-$\frac{1}{2}$×1×3=$\frac{7}{2}$;
故答案为:$\frac{7}{2}$;
(2)如图:
此时S△ABC=2a×4a-$\frac{1}{2}$a×2a-$\frac{1}{2}$×2a×2a-$\frac{1}{2}$=3a2;
(3)构造△ABC,如图所示,
此时S△ABC=3m×4n-$\frac{1}{2}$-$\frac{1}{2}$×3m×2n-$\frac{1}{2}$×2m×2n=5mn.
点评 此题考查了勾股定理,解题的关键是结合网格用矩形及容易求得面积的直角三角形表示出所求三角形的面积进行解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.若点(2,3)在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,那么下列各点在图象上的是( )
| A. | (-2,3) | B. | (1,5) | C. | (1,6) | D. | (1,-6) |
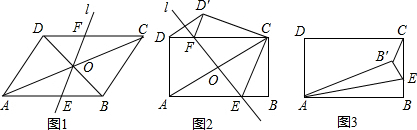
 如图,在?ABCD中,E,F分别是边AB,CD的中点,BD是对角线,AG∥BD交GB的延长线于点G.
如图,在?ABCD中,E,F分别是边AB,CD的中点,BD是对角线,AG∥BD交GB的延长线于点G.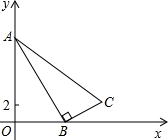 如图,已知Rt△ABC,∠ABC=90°,点A在y轴上,点B在x轴上,AB=10,BC=5,点C(m,3).
如图,已知Rt△ABC,∠ABC=90°,点A在y轴上,点B在x轴上,AB=10,BC=5,点C(m,3).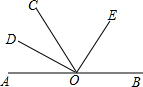 如图所示,直线AB上有一点O,由O点引出一条射线OC,作∠AOC,∠BOC的平分线OD,OE.OD和OE垂直吗?若OC在转动,其他条件不变,上述条件成立吗?
如图所示,直线AB上有一点O,由O点引出一条射线OC,作∠AOC,∠BOC的平分线OD,OE.OD和OE垂直吗?若OC在转动,其他条件不变,上述条件成立吗?