题目内容
4.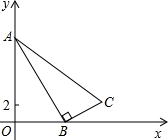 如图,已知Rt△ABC,∠ABC=90°,点A在y轴上,点B在x轴上,AB=10,BC=5,点C(m,3).
如图,已知Rt△ABC,∠ABC=90°,点A在y轴上,点B在x轴上,AB=10,BC=5,点C(m,3).(1)分别求点A、B的坐标及m的值;
(2)在第一象限中,画出以原点O为位似中心,将△ABC缩小后所得的△DEF,使△DEF与△ABC的对应边之比1:2.
分析 (1)利用已知得出△AOB∽△BMC,进而求出BO,AO的长即可得出m的值;
(2)利用位似图形的性质得出对应点位置即可得出答案.
解答 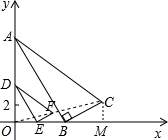 解:(1)过点C作CM⊥x轴于点M,
解:(1)过点C作CM⊥x轴于点M,
∵∠ABC=90°,
∴∠ABO+∠CBM=90°,
∵∠CBM+∠BCM=90°,
∴∠ABO=∠BCM,
∵∠AOB=∠CMB,
∴△AOB∽△BMC,
∴$\frac{AB}{BC}$=$\frac{BO}{MC}$=2,
∴$\frac{BO}{3}$=2,
解得:BO=6,
则AO=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴A(0,8),B(6,0),
则BM=$\frac{1}{2}$AO=4,
故m=4+6=10;
(2)如图所示:△DEF即为所求.
点评 此题主要考查了相似三角形的判定与性质以及位似变换,得出△AOB∽△BMC是解题关键.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
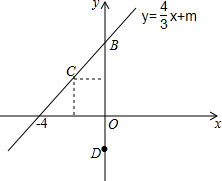 如图,已知一次函数y=$\frac{4}{3}$x+m的图象与x轴交于A(-6,0),交y轴于点B.
如图,已知一次函数y=$\frac{4}{3}$x+m的图象与x轴交于A(-6,0),交y轴于点B.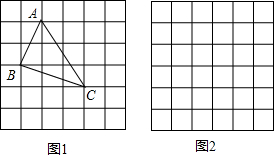
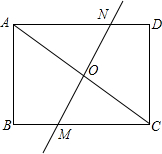 如图,把矩形ABCD沿直线MN对折,使点A,C重合,直线MN交AC于点O.求证:△COM∽△CBA.
如图,把矩形ABCD沿直线MN对折,使点A,C重合,直线MN交AC于点O.求证:△COM∽△CBA.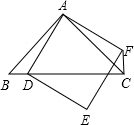 如图所示,四边形ADEF为正方形,△ABC为等腰直角三角形,D在BC边上,连接CF.
如图所示,四边形ADEF为正方形,△ABC为等腰直角三角形,D在BC边上,连接CF.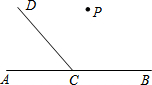 按照要求画图
按照要求画图 如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,以点B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论:
如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,以点B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论: