题目内容
14.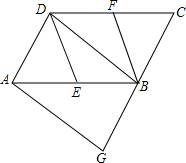 如图,在?ABCD中,E,F分别是边AB,CD的中点,BD是对角线,AG∥BD交GB的延长线于点G.
如图,在?ABCD中,E,F分别是边AB,CD的中点,BD是对角线,AG∥BD交GB的延长线于点G.(1)求证:四边形DAGB是平行四边形;
(2)求证:四边形DEBF是平行四边形;
(3)当四边形DEBF是菱形时,试判断四边形DAGB是何种特殊的平行四边形,并说明理由.
分析 (1)利用两组对边分别平行的四边形是平行四边形进而求出即可;
(2)利用一组对边平行且相等的四边形是平行四边形进而得出即可;
(3)利用菱形的性质得出DE=BE,再利用矩形的判定方法得出即可.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
又∵AG∥BD,
∴四边形DAGB是平行四边形;
(2)证明:∵四边形ABCD是平行四边形,
∴CD∥BA,AB=DC,
∵E,F分别是边AB,CD的中点,
∴DF$\stackrel{∥}{=}$BE,
∴四边形DEBF是平行四边形;
(3)解:当四边形DEBF是菱形时,四边形DAGB是矩形,
理由:∵四边形DEBF是菱形,
∴DE=BE,
∵AE=BE,
∴△ADB是直角三角形,
∴∠ADB=90°,
∵四边形DAGB是平行四边形,
∴平行四边形DAGB是矩形.
点评 此题主要考查了平行四边形的判定与性质以及菱形的性质和矩形的判定等知识,熟练掌握矩形的判定方法是解题关键.

练习册系列答案
相关题目
3.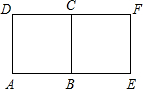 如图,由正方形ABCD通过一次旋转得到正方形BCFE,其可能的旋转中心有( )个.
如图,由正方形ABCD通过一次旋转得到正方形BCFE,其可能的旋转中心有( )个.
 如图,由正方形ABCD通过一次旋转得到正方形BCFE,其可能的旋转中心有( )个.
如图,由正方形ABCD通过一次旋转得到正方形BCFE,其可能的旋转中心有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点.
如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点.
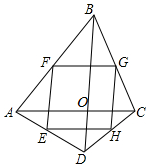 如图,四边形ABCD中,AC⊥BD于O,点E,F,G,H分别为AD,AB,BC,CD的中点.
如图,四边形ABCD中,AC⊥BD于O,点E,F,G,H分别为AD,AB,BC,CD的中点.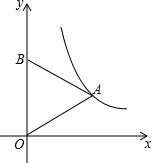 如图,等边三角形OAB的顶点A在反比例函数y=$\frac{\sqrt{3}}{x}$的图象上,点B在y轴上,若将△OAB沿x轴正方向平移,当点B落在反比例函数的图象上时,点A的坐标为($\frac{3\sqrt{3}}{2}$,1).
如图,等边三角形OAB的顶点A在反比例函数y=$\frac{\sqrt{3}}{x}$的图象上,点B在y轴上,若将△OAB沿x轴正方向平移,当点B落在反比例函数的图象上时,点A的坐标为($\frac{3\sqrt{3}}{2}$,1).