题目内容
9.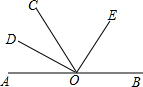 如图所示,直线AB上有一点O,由O点引出一条射线OC,作∠AOC,∠BOC的平分线OD,OE.OD和OE垂直吗?若OC在转动,其他条件不变,上述条件成立吗?
如图所示,直线AB上有一点O,由O点引出一条射线OC,作∠AOC,∠BOC的平分线OD,OE.OD和OE垂直吗?若OC在转动,其他条件不变,上述条件成立吗?
分析 结合题意和图形,运用平角的定义和角平分线的定义,证明∠EOD是90°,得直线OE、OD的位置关系.
解答 解:垂直,理由如下:
∵射线OC把平角∠AOB分成两个角,
∴∠AOC+∠BOC=180°,
又∵OD,OE分别是∠BOC和∠AOC的平分线,
∴∠EOC=$\frac{1}{2}$∠AOC,∠DOC=$\frac{1}{2}$∠BOC,
∴∠EOD=∠EOC+∠DOC=$\frac{1}{2}$(∠BOC+∠AOC)=90°,
∴OE和OD的位置关系是垂直;
当OC在转动,其他条件不变,上述条件仍成立.
点评 此题考查垂直的定义,利用垂直的定义除了由垂直得直角外,还能由直角判定垂直,判断两直线的夹角是否为90°是判断两直线是否垂直的基本方法.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
20.点A为数轴上表示-4的动点,当点A沿数轴移动4个单位长到B时,点B所表示的实数是( )
| A. | 0 | B. | -8或0 | C. | 0 | D. | 不同于以上答案 |
1. 如图,∠1和∠2互补,∠3=130°,那么∠4的度数是( )
如图,∠1和∠2互补,∠3=130°,那么∠4的度数是( )
 如图,∠1和∠2互补,∠3=130°,那么∠4的度数是( )
如图,∠1和∠2互补,∠3=130°,那么∠4的度数是( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
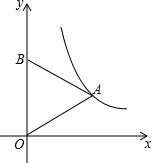 如图,等边三角形OAB的顶点A在反比例函数y=$\frac{\sqrt{3}}{x}$的图象上,点B在y轴上,若将△OAB沿x轴正方向平移,当点B落在反比例函数的图象上时,点A的坐标为($\frac{3\sqrt{3}}{2}$,1).
如图,等边三角形OAB的顶点A在反比例函数y=$\frac{\sqrt{3}}{x}$的图象上,点B在y轴上,若将△OAB沿x轴正方向平移,当点B落在反比例函数的图象上时,点A的坐标为($\frac{3\sqrt{3}}{2}$,1). 如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,以点B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论:
如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,以点B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论: 四边形ABCD的两条对角线相交于点O,AB∥CD,且AB=CD,S△AOB=5,则四边形ABCD的面积为20.
四边形ABCD的两条对角线相交于点O,AB∥CD,且AB=CD,S△AOB=5,则四边形ABCD的面积为20.