题目内容
18.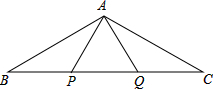 如图,P、Q是△ABC的边BC上的两点,且BP=AP=AQ=QC=PQ,则∠BAC=( )
如图,P、Q是△ABC的边BC上的两点,且BP=AP=AQ=QC=PQ,则∠BAC=( )| A. | 90° | B. | 120° | C. | 125° | D. | 130° |
分析 如图,首先证明∠B=∠BAP(设为α),∠C=∠QAC(设为β);其次证明∠APQ=∠AQP=∠PAQ=60°,借助三角形外角的性质,即可解决问题.
解答  解:如图,∵BP=AP=AQ=QC=PQ,
解:如图,∵BP=AP=AQ=QC=PQ,
∴∠B=∠BAP(设为α),∠C=∠QAC(设为β),△APQ为等边三角形,
∴∠APQ=∠AQP=∠PAQ=60°,
∵∠APQ=∠B+∠BAP=2α,
∴α=30°;
同理可求β=30°,
∴∠BAC=60°+2×30°=120°.
故选B.
点评 该题以三角形为载体,以等腰三角形的性质、三角形的内角和定理、外角的性质等为考查的核心构造而成;牢固掌握等腰三角形的性质、三角形的内角和定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
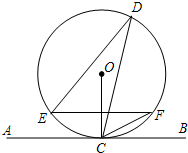 如图,直线AB切⊙O于点C,D是⊙O上一点,∠EDC=30°,弦EF∥AB,连接OC交EF于点H,连接CF,且CF=2,则EF的长为2$\sqrt{3}$.
如图,直线AB切⊙O于点C,D是⊙O上一点,∠EDC=30°,弦EF∥AB,连接OC交EF于点H,连接CF,且CF=2,则EF的长为2$\sqrt{3}$. 如图,在△ABC和△DEF中,若AB>BC,且AB=AC=EF,BC=DE=DF,∠A=∠E=∠F,则∠D=108°.
如图,在△ABC和△DEF中,若AB>BC,且AB=AC=EF,BC=DE=DF,∠A=∠E=∠F,则∠D=108°.