题目内容
3.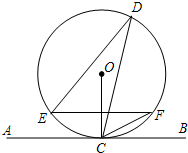 如图,直线AB切⊙O于点C,D是⊙O上一点,∠EDC=30°,弦EF∥AB,连接OC交EF于点H,连接CF,且CF=2,则EF的长为2$\sqrt{3}$.
如图,直线AB切⊙O于点C,D是⊙O上一点,∠EDC=30°,弦EF∥AB,连接OC交EF于点H,连接CF,且CF=2,则EF的长为2$\sqrt{3}$.
分析 根据切线的性质知道OC⊥AB,根据EF∥AB,得出OC⊥EF,根据圆周角的性质得到∠D=∠F=30°,根据垂径定理得到OC垂直平分EF,最后利用$\frac{1}{2}$EF=CF•cos30°即可求出EF.
解答 解:∵直线AB切⊙O于点C,
∴OC⊥AB,
∵EF∥AB,
∴OC⊥EF,
∴OC垂直平分EF,
∵∠F=∠D=30°,
∴$\frac{1}{2}$EF=CF•cos30°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴EF=2$\sqrt{3}$.
故答案为2$\sqrt{3}$.
点评 本题考查了切线的性质,平行线的性质,直角三角形的性质,余弦的概念等,综合性比较强,熟练掌握性质定理是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
11.泰州和姜堰某厂同时生产有某种型号的机器若干台,泰州厂可支援外地10台,姜堰厂可支援外地4台,兴化需要该种型号机器8台,泰兴需要6台,每台机器的运费(单位:元)如下表,设泰州运往兴化的机器为x台.
(1)用x的代数式表示:
(2)泰州运往兴化的运费是400x元
(3)若运这批机器的总运费为6800元,则泰州运往兴化的机器应为多少台?
| 终点 起点 | 泰兴 | 兴化 |
| 姜堰厂 | 300 | 500 |
| 泰州厂 | 600 | 400 |
| 终点 起点 | 泰兴 | 兴化 |
| 姜堰厂 | x-4 | 8-x |
| 泰州厂 | 10-x | x |
(3)若运这批机器的总运费为6800元,则泰州运往兴化的机器应为多少台?
18.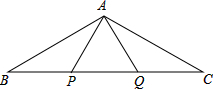 如图,P、Q是△ABC的边BC上的两点,且BP=AP=AQ=QC=PQ,则∠BAC=( )
如图,P、Q是△ABC的边BC上的两点,且BP=AP=AQ=QC=PQ,则∠BAC=( )
 如图,P、Q是△ABC的边BC上的两点,且BP=AP=AQ=QC=PQ,则∠BAC=( )
如图,P、Q是△ABC的边BC上的两点,且BP=AP=AQ=QC=PQ,则∠BAC=( )| A. | 90° | B. | 120° | C. | 125° | D. | 130° |
 如图,在?ABCD中,∠A的平分线交BC于E,若AB=10cm,AD=12cm,则EC=2cm.
如图,在?ABCD中,∠A的平分线交BC于E,若AB=10cm,AD=12cm,则EC=2cm.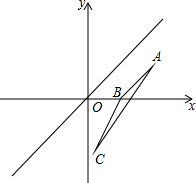 已知直线l平分∠xOy,△ABC与△A1B1C1关于直线l对称.
已知直线l平分∠xOy,△ABC与△A1B1C1关于直线l对称. 如图,∠CAB中,点A、B、C均在6×6的正方形网格格点上,请用无刻度的直尺画出的∠CAB平分线,并说明理由.
如图,∠CAB中,点A、B、C均在6×6的正方形网格格点上,请用无刻度的直尺画出的∠CAB平分线,并说明理由.