题目内容
8.在数轴上,-2对应的点为A,点B与点A的距离为$\sqrt{7}$,则点B表示的数为$\sqrt{7}$-2或-$\sqrt{7}$-2.分析 设B点表示的数是x,再根据数轴上两点间的距离公式即可得出结论.
解答 解:设B点表示的数是x,
∵-2对应的点为A,点B与点A的距离为$\sqrt{7}$,
∴|x+2|=$\sqrt{7}$,
解得x=$\sqrt{7}$-2或x=-$\sqrt{7}$-2.
故答案为:$\sqrt{7}$-2或-$\sqrt{7}$-2.
点评 本题考查的是实数与数轴,熟知数轴上两点间的距离公式是解答此题的关键.

练习册系列答案
相关题目
16.已知P(x,y)的坐标满足方程|x+1|+$\sqrt{y-2}$=0,则P点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3. 通过平移后可以得到的图的是( )
通过平移后可以得到的图的是( )
 通过平移后可以得到的图的是( )
通过平移后可以得到的图的是( )| A. |  | B. |  | C. |  | D. |  |
18.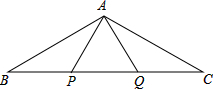 如图,P、Q是△ABC的边BC上的两点,且BP=AP=AQ=QC=PQ,则∠BAC=( )
如图,P、Q是△ABC的边BC上的两点,且BP=AP=AQ=QC=PQ,则∠BAC=( )
 如图,P、Q是△ABC的边BC上的两点,且BP=AP=AQ=QC=PQ,则∠BAC=( )
如图,P、Q是△ABC的边BC上的两点,且BP=AP=AQ=QC=PQ,则∠BAC=( )| A. | 90° | B. | 120° | C. | 125° | D. | 130° |
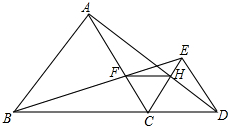 如图,已知点B,C,D在同一条直线上,△ABC和△CDE都是等边三角形,BE交AC于点F,AD交CE于点H.
如图,已知点B,C,D在同一条直线上,△ABC和△CDE都是等边三角形,BE交AC于点F,AD交CE于点H.