题目内容
6.列分式方程解应用题:秋冬交界时节,我国雾霾天气频发.由于市场需求,甲、乙两公司准备合作生产一批防雾箍口罩,12天可以完成;如果甲、乙两公司单独完成此项任务,乙公司所用时间是甲公司的1.5倍,求甲、乙公司单独完成此项工作各需多少天?分析 设甲公司单独完成此工作x天,则乙公司单独完成此项工作1.5x天,根据甲乙两公司合作,12天可以完成,列方程求解.
解答 解:设甲公司单独完成此工程x天,则乙公司单独完成此项工程1.5x天,
根据题意,得$\frac{1}{x}$+$\frac{1}{1.5x}$=$\frac{1}{12}$,
解得:x=20,
经检验,x=20是方程的解且符合题意,
1.5x=30.
答:甲、乙两公司单独完成此工程各需要20天,30天.
点评 本题考查了分式方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程求解,注意检验.

练习册系列答案
相关题目
16.已知P(x,y)的坐标满足方程|x+1|+$\sqrt{y-2}$=0,则P点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.泰州和姜堰某厂同时生产有某种型号的机器若干台,泰州厂可支援外地10台,姜堰厂可支援外地4台,兴化需要该种型号机器8台,泰兴需要6台,每台机器的运费(单位:元)如下表,设泰州运往兴化的机器为x台.
(1)用x的代数式表示:
(2)泰州运往兴化的运费是400x元
(3)若运这批机器的总运费为6800元,则泰州运往兴化的机器应为多少台?
| 终点 起点 | 泰兴 | 兴化 |
| 姜堰厂 | 300 | 500 |
| 泰州厂 | 600 | 400 |
| 终点 起点 | 泰兴 | 兴化 |
| 姜堰厂 | x-4 | 8-x |
| 泰州厂 | 10-x | x |
(3)若运这批机器的总运费为6800元,则泰州运往兴化的机器应为多少台?
18.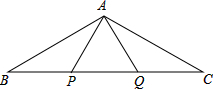 如图,P、Q是△ABC的边BC上的两点,且BP=AP=AQ=QC=PQ,则∠BAC=( )
如图,P、Q是△ABC的边BC上的两点,且BP=AP=AQ=QC=PQ,则∠BAC=( )
 如图,P、Q是△ABC的边BC上的两点,且BP=AP=AQ=QC=PQ,则∠BAC=( )
如图,P、Q是△ABC的边BC上的两点,且BP=AP=AQ=QC=PQ,则∠BAC=( )| A. | 90° | B. | 120° | C. | 125° | D. | 130° |
 如图,在?ABCD中,∠A的平分线交BC于E,若AB=10cm,AD=12cm,则EC=2cm.
如图,在?ABCD中,∠A的平分线交BC于E,若AB=10cm,AD=12cm,则EC=2cm.