题目内容
9. 如图,点A,F,C,D在同一直线上,点B与点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC,求证:BC=EF.
如图,点A,F,C,D在同一直线上,点B与点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC,求证:BC=EF.
分析 证出AC=DF,由SAS推出△ABC≌△DEF,由全等三角形的性质推出即可.
解答 证明:∵AF=DC,
∴AF+CF=DC+CF,
即AC=DF,
在△ABC和△DEF中,$\left\{\begin{array}{l}{AB=DF}&{\;}\\{∠A=∠D}&{\;}\\{AC=DF}&{\;}\end{array}\right.$,
∴△ABC≌△DEF(SAS),
∴BC=EF.
点评 本题考查了全等三角形的判定与性质;解此题的关键是推出△ABC≌△DEF,注意:全等三角形的对应边相等.

练习册系列答案
相关题目
17.庐阳区是合肥市政治、经济、文化、金融中心,常住人口62.5万,其中数字62.5万用科学记数法表示为( )
| A. | 62.5×104 | B. | 62.5×105 | C. | 6.25×106 | D. | 6.25×105 |
14.如果两圆的半径分别为2cm和5cm,圆心距为6cm,那么这两个圆的位置关系是( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
18.用白铁皮做罐头盒,每张白铁皮可制作成8个盒身或制作成24个盒底,一个盒身与两个盒底配成一套罐头盒,现有140张白铁皮,用多少张白铁皮制作盒身、多少张白铁皮制作盒底可以正好制作整套罐头盒而无余料?
19.重庆新天地陶瓷厂计划一周生产陶瓷工艺品350个,平均每天生产50个,但实际每天生产量与计划相比有出入,下表是某周的生产情况(以50个为标准,超产记为正、减产记为负):
(1)根据记录的数据,请直接写出该厂本周产量最多的一天比最少的一天多生产的工艺品的个数;
(2)该工艺厂在本周实际生产工艺品的数量为多少个?(列式计算)
(3)已知该厂实行每周计件工资制,每周结算一次,每生产一个工艺品可得5元,若超额完成任务(以350个为标准),则超过部分每个另奖10元,少生产每个扣3元,试求该工艺厂在这一周应付出的工资总额.
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减(单位:个) | +5 | -6 | -5 | +15 | -10 | +16 | -8 |
(2)该工艺厂在本周实际生产工艺品的数量为多少个?(列式计算)
(3)已知该厂实行每周计件工资制,每周结算一次,每生产一个工艺品可得5元,若超额完成任务(以350个为标准),则超过部分每个另奖10元,少生产每个扣3元,试求该工艺厂在这一周应付出的工资总额.
 如图,在等腰△ABC中,∠ABC=90°,D为AC边的中点,过D作DE⊥DF,交AB于E,交BC于F,BC=7,CF=3,求EF的长.
如图,在等腰△ABC中,∠ABC=90°,D为AC边的中点,过D作DE⊥DF,交AB于E,交BC于F,BC=7,CF=3,求EF的长.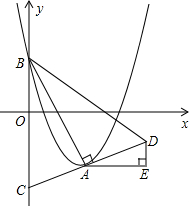 如图,在平面直角坐标系xOy中,抛物线y=(x-m)2-m2+m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.
如图,在平面直角坐标系xOy中,抛物线y=(x-m)2-m2+m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.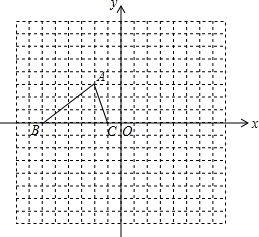 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).