题目内容
18.用白铁皮做罐头盒,每张白铁皮可制作成8个盒身或制作成24个盒底,一个盒身与两个盒底配成一套罐头盒,现有140张白铁皮,用多少张白铁皮制作盒身、多少张白铁皮制作盒底可以正好制作整套罐头盒而无余料?分析 根据题意可知题目中的等量关系:制盒身铁皮的张数×每张铁皮可制盒身的个数=制盒底铁皮的张数×每张铁皮可制盒底的个数÷2,据此解答.
解答 解:设用x张白铁皮制作盒身正好制作整套罐头盒而无余料,由题意得:
2×8x=24(140-x)
解得x=84
140-x=56
答:用84张白铁皮制作盒身,56张白铁皮制作盒底正好制作整套罐头盒而无余料.
点评 此题考查一元一次方程的实际运用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程解决问题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
3.若x2+2mx+36是完全平方式,则m=( )
| A. | 6 | B. | ±6 | C. | 12 | D. | ±12 |
7.已知一个多项式减去-2m结果等于m2+3m+2,这个多项式是( )
| A. | m2+5m+2 | B. | m2-m-2 | C. | m2-5m-2 | D. | m2+m+2 |
 如图,点A,F,C,D在同一直线上,点B与点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC,求证:BC=EF.
如图,点A,F,C,D在同一直线上,点B与点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC,求证:BC=EF.
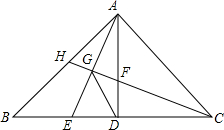 如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC于D,点E是线段BD上一点,连接AE,CH⊥AE交AD于F,交AE于G,交AB于H,连接GD.
如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC于D,点E是线段BD上一点,连接AE,CH⊥AE交AD于F,交AE于G,交AB于H,连接GD.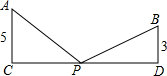 如图,A、B两个工厂合用的一个变压器位于P处,两厂位于过P的笔直高压输电线的同一侧,P到A、B两厂的距离相等,A、B两厂到高压线的距离分别为AC、BD,且AC=5千米,BD=3千米.如果CD=16千米,那么变压器所在处P与C处的距离是多少千米?
如图,A、B两个工厂合用的一个变压器位于P处,两厂位于过P的笔直高压输电线的同一侧,P到A、B两厂的距离相等,A、B两厂到高压线的距离分别为AC、BD,且AC=5千米,BD=3千米.如果CD=16千米,那么变压器所在处P与C处的距离是多少千米?