题目内容
20.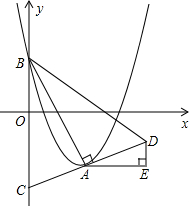 如图,在平面直角坐标系xOy中,抛物线y=(x-m)2-m2+m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.
如图,在平面直角坐标系xOy中,抛物线y=(x-m)2-m2+m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.(1)当m=2时,求点B的坐标;
(2)求DE的长?
分析 (1)将m=2代入抛物线解析式,再将x=0代入抛物线解析式求出y值,由此得出B点坐标;(2)借助三角形的相等找出AE的长度,再根据相似三角形边的比等于相似比即可得出结论.
解答 解:(1)当m=2时,抛物线解析式为y=(x-2)2-2.
把x=0代入y=(x-2)2-2,得:y=2.
∴点B的坐标为(0,2).
(2)延长EA,交y轴于点F,如图.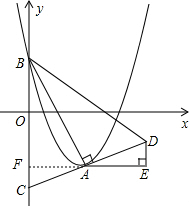
在△ADE和△ACF中,$\left\{\begin{array}{l}{∠AFC=∠AED=90°}\\{∠CAF=∠DAE}\\{AD=AC}\end{array}\right.$,
∴△AFC≌△AED,
∴AF=AE.
∵点A(m,-m2+m),点B(0,m),
∴AF=AE=|m|,BF=m-(-m2+m)=m2.
∵∠ABF=90°-∠BAF=∠DAE,∠AFB=∠DEA=90°,
∴△ABF∽△DAE,
∴$\frac{BF}{AF}$=$\frac{AE}{DE}$,即:$\frac{{m}^{2}}{|m|}$=$\frac{|m|}{DE}$,
∴DE=1.
点评 本题考查了二次函数的综合应用、全等三角形的判定及性质和相似三角形的判定及性质,解题的关键是:(1)代入m=2和x=0求取y值;(2)由三角形全等用m表示出线段AE,再结合相似三角形的性质找出DE的长.本题属于中档题,失分点在于(2)中求DE的长度,部分同学感觉无从下手,解决该类题型一般都是用到相似三角形的性质,可寻找含所求量的三角形及其相似三角形,借助相似比来得以解决.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10. 如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC=28°,则∠AOC的大小是( )
如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC=28°,则∠AOC的大小是( )
 如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC=28°,则∠AOC的大小是( )
如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC=28°,则∠AOC的大小是( )| A. | 28° | B. | 42° | C. | 56° | D. | 70° |
11.-0.2的倒数是( )
| A. | 0.2 | B. | -2 | C. | -$\frac{1}{5}$ | D. | -5 |
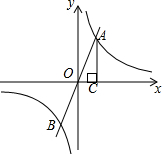 如图,已知点A(x,y)为反比例函数y=$\frac{k}{x}$(k>0)图象位于第一象限上一点,射线AO交双曲线y=$\frac{k}{x}$的另一支于点B,过点A作AC⊥x轴,连接BC.当点A的横坐标x逐渐增大时,则△ABC的面积( )
如图,已知点A(x,y)为反比例函数y=$\frac{k}{x}$(k>0)图象位于第一象限上一点,射线AO交双曲线y=$\frac{k}{x}$的另一支于点B,过点A作AC⊥x轴,连接BC.当点A的横坐标x逐渐增大时,则△ABC的面积( ) 如图,点A,F,C,D在同一直线上,点B与点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC,求证:BC=EF.
如图,点A,F,C,D在同一直线上,点B与点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC,求证:BC=EF.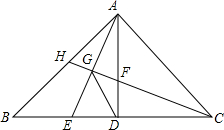 如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC于D,点E是线段BD上一点,连接AE,CH⊥AE交AD于F,交AE于G,交AB于H,连接GD.
如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC于D,点E是线段BD上一点,连接AE,CH⊥AE交AD于F,交AE于G,交AB于H,连接GD.