题目内容
7.已知关于x的一元二次方程x2+2x+m=0(1)当m=8时,判断方程的根的情况;
(2)当m=-8时,求方程的根.
分析 (1)将m=8代入原方程,根据根的判别式b2-4ac=-28<0,即可得知原方程没有实数根;
(2)将m=-8代入原方程,利用十字相乘法分解因式,即可得出结论.
解答 解:(1)当m=8时,b2-4ac=22-4×1×8=4-32=-28<0,
∴原方程没有实数根.
(2)当m=-8时,原方程为x2+2x-8=0,
即(x-2)(x+4)=0,
∴x1=2,x2=-4.
点评 本题考查了根的判别式以及十字相乘法解方程,解题的关键是:(1)由根的判别式b2-4ac<0得出方程没有实数根;(2)将原方程变形为(x-2)(x+4)=0.本题属于基础题,难度不大,解决该题型题目时,利用根的判别式判定方程实数根的个数是关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
15.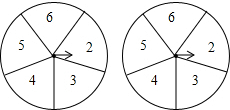 如图的两个圆盘中均有5个数字,同时旋转两个圆盘,指针落在某一个数上的机会均等,那么两个指针同时落在奇数上的概率是( )
如图的两个圆盘中均有5个数字,同时旋转两个圆盘,指针落在某一个数上的机会均等,那么两个指针同时落在奇数上的概率是( )
 如图的两个圆盘中均有5个数字,同时旋转两个圆盘,指针落在某一个数上的机会均等,那么两个指针同时落在奇数上的概率是( )
如图的两个圆盘中均有5个数字,同时旋转两个圆盘,指针落在某一个数上的机会均等,那么两个指针同时落在奇数上的概率是( )| A. | $\frac{4}{25}$ | B. | $\frac{6}{25}$ | C. | $\frac{10}{25}$ | D. | $\frac{19}{25}$ |
2.方程x2-2x+3=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 没有实数根 | ||
| C. | 有两个不相等的实数根 | D. | 只有一个实数根 |
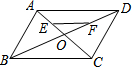 如图,在平行四边形ABCD中,AC与BD相交于点O,点E、F分别是OA、OD的中点,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BO}$=$\overrightarrow{b}$,那么$\overrightarrow{EF}$=$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$.
如图,在平行四边形ABCD中,AC与BD相交于点O,点E、F分别是OA、OD的中点,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BO}$=$\overrightarrow{b}$,那么$\overrightarrow{EF}$=$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$.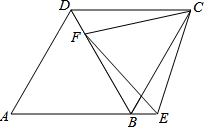 如图,在菱形ABCD中,F为对角线BD上一点,点E为AB延长线上一点,DF=BE,CE=CF.求证:
如图,在菱形ABCD中,F为对角线BD上一点,点E为AB延长线上一点,DF=BE,CE=CF.求证: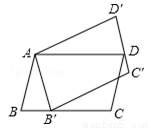
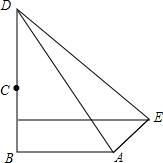 已知山顶上有一塔,山高BC为110米,小明在坡比为3:4的斜坡AE的底部A点测得塔顶D的仰角为45°,当他沿斜坡上行100米到达E时,测得塔顶D的仰角为19°,AB在同一水平线上,求塔高CD.(参考数据:tan19°≈0.35)
已知山顶上有一塔,山高BC为110米,小明在坡比为3:4的斜坡AE的底部A点测得塔顶D的仰角为45°,当他沿斜坡上行100米到达E时,测得塔顶D的仰角为19°,AB在同一水平线上,求塔高CD.(参考数据:tan19°≈0.35)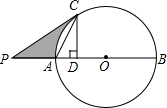 如图,已知⊙O的直径AB=10cm,C是⊙O上的一点,作CD⊥AB于点D,以C为顶点作∠PCA=∠ACD,交BA的延长线于点P,
如图,已知⊙O的直径AB=10cm,C是⊙O上的一点,作CD⊥AB于点D,以C为顶点作∠PCA=∠ACD,交BA的延长线于点P,