题目内容
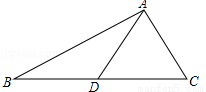
10.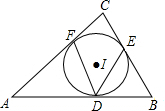 如图:⊙I内切于△ABC,切点分别为D、E、F,若∠A=50°,∠B=60°,连接DE,DE,则∠EDF=55°.
如图:⊙I内切于△ABC,切点分别为D、E、F,若∠A=50°,∠B=60°,连接DE,DE,则∠EDF=55°.
分析 连IF,IE,由切线性质得∠IFC=∠IEC=90°,根据四边形的内角和定理即可求得∠FIE的度数,然后利用圆周角定理即可求得.
解答 解:连IF,IE,如图所示: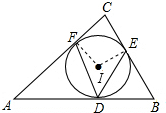
由切线性质得∠IFC=∠IEC=90°,
∵∠A=50°,∠B=60°,
∴∠C=180°-50°-60°=70°,
∴∠FIE=180°-∠C=110°,
∴∠FDE=$\frac{1}{2}$∠FIE=$\frac{1}{2}$×110°=55°.
故答案为:55°.
点评 本题考查了切线的性质,三角形内角和定理以及圆周角定理;熟记切线的性质,由圆周角定理得出结果是解决问题的关键.

练习册系列答案
相关题目
15.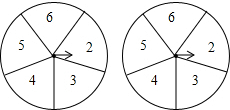 如图的两个圆盘中均有5个数字,同时旋转两个圆盘,指针落在某一个数上的机会均等,那么两个指针同时落在奇数上的概率是( )
如图的两个圆盘中均有5个数字,同时旋转两个圆盘,指针落在某一个数上的机会均等,那么两个指针同时落在奇数上的概率是( )
 如图的两个圆盘中均有5个数字,同时旋转两个圆盘,指针落在某一个数上的机会均等,那么两个指针同时落在奇数上的概率是( )
如图的两个圆盘中均有5个数字,同时旋转两个圆盘,指针落在某一个数上的机会均等,那么两个指针同时落在奇数上的概率是( )| A. | $\frac{4}{25}$ | B. | $\frac{6}{25}$ | C. | $\frac{10}{25}$ | D. | $\frac{19}{25}$ |
2.方程x2-2x+3=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 没有实数根 | ||
| C. | 有两个不相等的实数根 | D. | 只有一个实数根 |
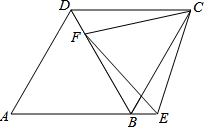 如图,在菱形ABCD中,F为对角线BD上一点,点E为AB延长线上一点,DF=BE,CE=CF.求证:
如图,在菱形ABCD中,F为对角线BD上一点,点E为AB延长线上一点,DF=BE,CE=CF.求证: