题目内容
若点P、Q为线段AB的两个不同的黄金分割点,AB=10,则PQ= .
考点:黄金分割
专题:
分析:先根据黄金分割的定义得出较长的线段AP=BQ=
AB,再根据PQ=AP+BQ-AB,即可得出结果.
| ||
| 2 |
解答: 解:根据黄金分割点的概念,可知AP=BQ=
解:根据黄金分割点的概念,可知AP=BQ=
×10=(5
-5).
则PQ=AP+BQ-AB=(5
-5)×2-10=(10
-20).
故本题答案为:10
-20.
 解:根据黄金分割点的概念,可知AP=BQ=
解:根据黄金分割点的概念,可知AP=BQ=
| ||
| 2 |
| 5 |
则PQ=AP+BQ-AB=(5
| 5 |
| 5 |
故本题答案为:10
| 5 |
点评:此题主要是考查了黄金分割的概念:把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值(
)叫做黄金比.熟记黄金分割分成的两条线段和原线段之间的关系,能够熟练求解.
| ||
| 2 |

练习册系列答案
相关题目
下面四句关于约数和倍数的话中正确的是( )
| A、正整数a和b的最小公倍数一定小于ab |
| B、正整数a和b的最大公约数一定不大于a |
| C、正整数a和b的最小公倍数一定不小于ab |
| D、正整数a和b的最大公约数一定大于a |
若正六边形的外接圆的半径为R,则这个正六边形的面积为( )
A、
| ||||
| B、6R2 | ||||
C、
| ||||
| D、6R |
 如图,△ABE是边长为21的正三角形.已知四边形BCDE的周长是△ABE周长的两倍.则五边形ABCDE的周长是( )
如图,△ABE是边长为21的正三角形.已知四边形BCDE的周长是△ABE周长的两倍.则五边形ABCDE的周长是( )| A、137 | B、147 |
| C、157 | D、167 |
 如图,将△ABC绕点C旋转60°得到△A′B′C′,已知AC=6,BC=4,则线段AB扫过图形(阴影部分)的面积为
如图,将△ABC绕点C旋转60°得到△A′B′C′,已知AC=6,BC=4,则线段AB扫过图形(阴影部分)的面积为 若现在需要在电话中告诉你的同学如图的图形,你将怎么说?提供两种.
若现在需要在电话中告诉你的同学如图的图形,你将怎么说?提供两种.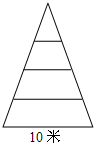 如图,是一轴截面为等腰三角形的古塔,塔基圆直径为10米,塔共四层,每层高3米,天意广告公司欲沿塔面悬挂一幅公益广告条幅,要求条幅不能铺在地面上,也不能高于塔顶,则条幅的最大长度为
如图,是一轴截面为等腰三角形的古塔,塔基圆直径为10米,塔共四层,每层高3米,天意广告公司欲沿塔面悬挂一幅公益广告条幅,要求条幅不能铺在地面上,也不能高于塔顶,则条幅的最大长度为