题目内容
16.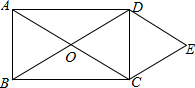 如图,在矩形ABCD中,对角线AC与BD交于点O,E是矩形ABCD外一点,且∠EDC=∠OCD,∠ECD=∠ODC,请说明CE=OA.
如图,在矩形ABCD中,对角线AC与BD交于点O,E是矩形ABCD外一点,且∠EDC=∠OCD,∠ECD=∠ODC,请说明CE=OA.
分析 先证明△ECD≌△ODC,从而得到CE=OD,然后由矩形的性质可知OD=OA,从而可证明CE=OA.
解答 解:在△ECD和△ODC中,$\left\{\begin{array}{l}{∠EDC=∠OCD}\\{CD=CD}\\{∠ECD=∠ODC}\end{array}\right.$,
∴△ECD≌△ODC.
∴CE=OD.
∵四边形ABCD是矩形,
∴OD=OA.
∴CE=OA.
点评 本题主要考查的是矩形的性质、全等三角形的性质和判定、掌握矩形的性质和全等三角形的判定定理是解题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
11.在△ABC中,点I是内心,∠BIC=114°,则∠A的度数为( )
| A. | 57° | B. | 66° | C. | 48° | D. | 78° |
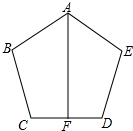 已知BC=ED,AB=AE,∠B=∠E,F是CD的中点,求证:AF⊥CD.
已知BC=ED,AB=AE,∠B=∠E,F是CD的中点,求证:AF⊥CD. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则不等式ax2+bx+c<0的解集是-1<x<3.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则不等式ax2+bx+c<0的解集是-1<x<3. 已知:如图,菱形ABCD的对角线AC和BD相交于点O.求证:菱形ABCD各边中点M,N,P,Q在以O为圆心的同一个圆上.
已知:如图,菱形ABCD的对角线AC和BD相交于点O.求证:菱形ABCD各边中点M,N,P,Q在以O为圆心的同一个圆上.