题目内容
19.如图1,在正方形ABCD中,P为对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F,连接CE.(1)求证:△PCE是等腰直角三角形;
(2)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,判断△PCE的形状,并说明理由.

分析 (1)由△PDA≌△PDC,推出PA=PC,∠3=∠1,由PA=PE,推出∠2=∠3,推出∠1=∠2,由∠EDF=90°,∠DFE=∠PFC,推出∠FPC=EDF=90°,推出△PEC是等腰直角三角形;
(2)由△PDA≌△PDC,推出PA=PC,∠3=∠1,由PA=PE,推出∠2=∠3,PA═PE=PC,推出∠1=∠2,由∠DFE=∠PFC,推出∠EPC=∠EDC,由∠ADC=120°,推出∠EDC=60°,推出∠EPC=60°,由PE=PC,即可证明△PEC是等边三角形;
解答 (1)证明:如图1中,
∵四边形ABCD是正方形,
∴AD=DC,∠ADB=∠CDB=45°,∠ADC=90°,
在△PDA和△PDC中,
$\left\{\begin{array}{l}{PD=PD}\\{∠PDA=∠PDC}\\{DA=DC}\end{array}\right.$,
∴△PDA≌△PDC,
∴PA=PC,∠3=∠1,
∵PA=PE,
∴∠2=∠3,
∴∠1=∠2,
∵∠EDF=90°,∠DFE=∠PFC,
∴∠FPC=EDF=90°,
∴△PEC是等腰直角三角形.
(2)解:如图2中,结论:△PCE是等边三角形.
理由:∵四边形ABCD是菱形,
∴AD=DC,∠ADB=∠CDB,∠ADC=∠ABC=120°,
在△PDA和△PDC中,
$\left\{\begin{array}{l}{PD=PD}\\{∠PDA=∠PDC}\\{DA=DC}\end{array}\right.$,
∴△PDA≌△PDC,
∴PA=PC,∠3=∠1,
∵PA=PE,
∴∠2=∠3,PA═PE=PC,
∴∠1=∠2,
∵∠DFE=∠PFC,
∴∠EPC=∠EDC,
∵∠ADC=120°,
∴∠EDC=60°,
∴∠EPC=60°,∵PE=PC,
∴△PEC是等边三角形.
点评 本题考查正方形的性质、菱形的性质、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.

 字词句段篇系列答案
字词句段篇系列答案 6张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
6张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )| A. | a=2b | B. | a=3b | C. | a=4b | D. | a=b |
| A. | 0 | B. | 1 | C. | 12 | D. | 24 |
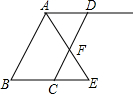 如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.请你判断AD和BE的位置关系,并说明理由.
如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.请你判断AD和BE的位置关系,并说明理由. 如图,A、B两点被池塘隔开,在AB外选一点C,连接AC、BC,取AC、BC的中点D、E,量出DE=a,则AB=2a,它的根据是三角形的中位线等于第三边的一半.
如图,A、B两点被池塘隔开,在AB外选一点C,连接AC、BC,取AC、BC的中点D、E,量出DE=a,则AB=2a,它的根据是三角形的中位线等于第三边的一半.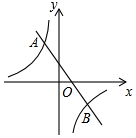 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$的图象与一次函数y=ax+b的图象交于点A(-2,3)和点B(m,-2).
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$的图象与一次函数y=ax+b的图象交于点A(-2,3)和点B(m,-2). 如图,已知,在矩形ABCD中,∠BAD的平分线分别与边BC及边DC的延长线相交于点E,F,G,点G为EF中点,连接DG.
如图,已知,在矩形ABCD中,∠BAD的平分线分别与边BC及边DC的延长线相交于点E,F,G,点G为EF中点,连接DG.