题目内容
17．
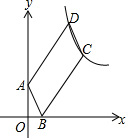如图，在直角坐标系中，平行四边形ABCD的顶点A（0，2）、B（1，0）在x轴、y轴上，另两个顶点C、D在第一象限内，且AD=3AB．若反比例函数$y=\frac{k}{x}$（k＞0）的图象经过C，D两点，则k的值是24．
分析 设D（x，$\frac{k}{x}$）（x＞0，k＞0），根据平行四边形的对边平行得到C（x+1，$\frac{k}{x}$-2）；然后由两点间的距离公式和反比例函数图象上点的横纵坐标的乘积等于k列出方程组，通过解方程组可以求得k的值．
解答 解：如图，∵在直角坐标系中，平行四边形ABCD的顶点A（0，2）、B（1，0），
∴CD=AB=$\sqrt{{2}^{2}+{1}^{2}}=\sqrt{5}$，AB∥CD．
又∵AD=3AB，
∴AD=3$\sqrt{5}$．
设D（x，$\frac{k}{x}$）（x＞0，k＞0），则C（x+1，$\frac{k}{x}$-2），
则$\left\{\begin{array}{l}{{x}^{2}+（\frac{k}{x}-2）^{2}=45}\\{k=（x+1）（\frac{k}{x}-2）}\end{array}\right.$，
解得$\left\{\begin{array}{l}{x=3}\\{k=24}\end{array}\right.$．
故答案是：24．
点评 本题考查了平行四边形的性质和反比例函数图象上点的坐标特征．图象上的点（x，y）的横纵坐标的积是定值k，即xy=k．
练习册系列答案
备战中考寒假系列答案
相关题目
一般情况下，学生注意力上课后逐渐增强，中间有段时间处于较理想的稳定状态，随后开始分散．实验结果表明，学生注意力指数y随时间x（min）的变化规律如图所示（其中AB、BC分别为线段，CD为双曲线的一部分）：
8．关于反比例函数y=-$\frac{4}{x}$，下列说法正确的是（ ）
| A． | 图象在第一、三象限 | B． | 图象经过点（2，-8） | ||
| C． | 当x＞0时，y随x的增大而减小 | D． | 当x＜0时，y随x的增大而增大 |
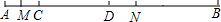如图，已知线段AB=14，在AB上有C，D，M，N四点，且满足AC：CD：DB=1：2：4，AC=2AM，DB=4DN．求：MN的长度．
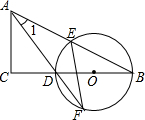如图，在△ABC中，∠C=90°，D是BC边上一点，以DB为直径的⊙O经过AB的中点E，交AD的延长线于点F，连结EF．