题目内容
16．在一个密闭不透明的袋子里有若干个白球．为估计白球个数，小何向其中投入8个黑球，搅拌均匀后随机摸出一个球，记下颜色，再把它放入袋中，不断重复摸球400次，其中88次摸到黑球，则估计袋中大约有白球（ ）| A． | 18个 | B． | 28个 | C． | 36个 | D． | 42个 |
分析 根据摸到黑球的概率和黑球的个数，可以求出袋中放入黑球后总的个数，然后再减去黑球个数，即可得到白球的个数．
解答 解：由题意可得，
白球的个数大约为：8÷$\frac{88}{400}$-8≈28，
故选B．
点评 本题考查用样本估计总体，解题的关键是明确题意，根据摸到黑球的概率求出总体．
练习册系列答案
相关题目
如图是由4个完全相同的小正方体组成的立体图形，则它的俯视图是（ ）
一般情况下，学生注意力上课后逐渐增强，中间有段时间处于较理想的稳定状态，随后开始分散．实验结果表明，学生注意力指数y随时间x（min）的变化规律如图所示（其中AB、BC分别为线段，CD为双曲线的一部分）：
11．
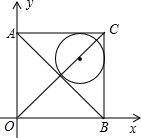如图，在平面直角坐标系中有一正方形AOBC，反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点，半径为4-2$\sqrt{2}$的圆内切于△ABC，则k的值为（ ）
如图，在平面直角坐标系中有一正方形AOBC，反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点，半径为4-2$\sqrt{2}$的圆内切于△ABC，则k的值为（ ）| A． | $\sqrt{2}$ | B． | 2 | C． | 4 | D． | 2$\sqrt{2}$ |
如图，已知点B，D在反比例函数y=$\frac{a}{x}$（a＞0）的图象上，点A，C在反比例函数y=$\frac{b}{x}$（b＜0）的图象上，AB∥CD∥x轴，AB，CD在x轴的同侧，AB=4，CD=3，AB与CD的距离为1，则a-b的值是12．
8．关于反比例函数y=-$\frac{4}{x}$，下列说法正确的是（ ）
| A． | 图象在第一、三象限 | B． | 图象经过点（2，-8） | ||
| C． | 当x＞0时，y随x的增大而减小 | D． | 当x＜0时，y随x的增大而增大 |
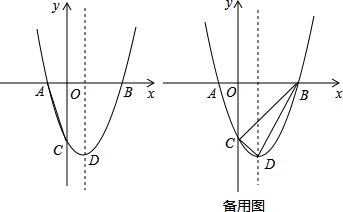
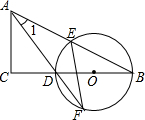如图，在△ABC中，∠C=90°，D是BC边上一点，以DB为直径的⊙O经过AB的中点E，交AD的延长线于点F，连结EF．