题目内容
12.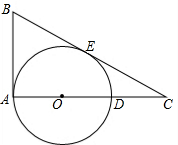 如图,在Rt△ABC中,∠BAC=90°,点O在AC上,BC切⊙O于点E,且AB=5,AC=12.
如图,在Rt△ABC中,∠BAC=90°,点O在AC上,BC切⊙O于点E,且AB=5,AC=12.(1)求切线CE的长;
(2)求⊙O的半径r.
分析 (1)连接BO、EO,利用勾股定理得出BC的长,再利用AB=BE解答即可;
(2)在本题中,要求圆的半径,须连接BO、EO,利用勾股定理求出线段AB的长,再利用面积的转化,继而求出圆的半径.
解答 解:(1)连接BO、EO,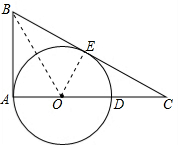 ∵∠BAC=90°,且AB=5,AC=12,
∵∠BAC=90°,且AB=5,AC=12,
∴BC=13,
∵点O在AC上,BC切⊙O于点E,
∴AB=BE=5,
∴CE=13-5=8;
(2)连接BO、EO,设⊙O半径为x,
在Rt△AB中,根据勾股定理,有:BC=$\sqrt{A{B}^{2}+A{C}^{2}}=\sqrt{{5}^{2}+1{2}^{2}}=13$,
则S△ABC=S△ABO+S△BCO,
则$\frac{1}{2}AC•AB=\frac{1}{2}AB•AO+\frac{1}{2}BC•EO$,
即$\frac{1}{2}×12×5=\frac{1}{2}×5x+\frac{1}{2}×13x$,
解得:x=$\frac{10}{3}$.
∴⊙O的半径是$\frac{10}{3}$.
点评 考查了求线段的长度常用的方法:
1.用勾股定理,适用于已知两边的直角三角形中;
2.用相似三角形,适用于有相似三角形的图形中;
3.面积法,适用于有直角三角形的图形中有高的存在.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
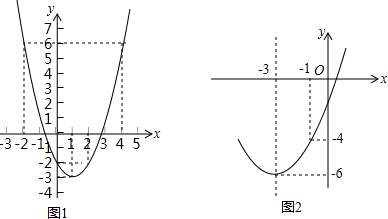
5.利用二次函数y=x2-2x-2的图象求一元二次方程y=x2-2x-2的近似解时,画图如图1示并进一步估算其中一根列表如下,根据这些信息,可得方程的正的近似根是( )
| x | -0.9 | -0.8 | -0.7 | -0.6 |
| y=x2-2x-2 | -0.61 | 0.24 | -0.11 | -0.44 |

| A. | 0.7 | B. | 2.6 | C. | 2.7 | D. | 2.8 |
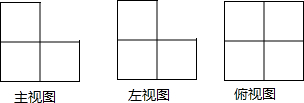
7.如图,是由几个相同的小正方体搭成的几何体的三种视图,则搭成这个几何体的小正方体的个数是( )

| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
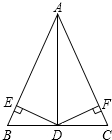 如图,在△ABC中,AB=AC,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF.请选择一对你认为全等的三角形并加以证明.
如图,在△ABC中,AB=AC,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF.请选择一对你认为全等的三角形并加以证明.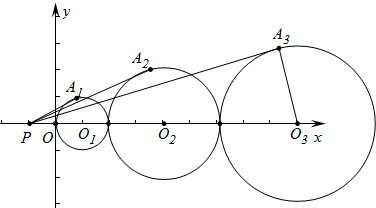 如图,点P(-1,0),以圆心在x轴正半轴上连续作圆,半径分别为1、2、3,过点P作圆的切线,切点分别为A1、A2、A3,则sin∠O3PA3=$\frac{3}{10}$.
如图,点P(-1,0),以圆心在x轴正半轴上连续作圆,半径分别为1、2、3,过点P作圆的切线,切点分别为A1、A2、A3,则sin∠O3PA3=$\frac{3}{10}$.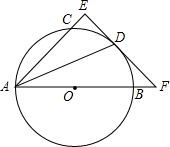 如图,AB是圆O的直径,点C、D在圆O上,且AD平分∠CAB.过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F.
如图,AB是圆O的直径,点C、D在圆O上,且AD平分∠CAB.过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F.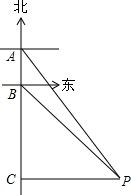 有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是7海里.(结果取整数)(参考数据:$\sqrt{3}$≈1.73)
有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是7海里.(结果取整数)(参考数据:$\sqrt{3}$≈1.73)