题目内容
8.已知x的一元二次方程x2+2(k-2)x+k2+4=0有两个实数根,设它的两个根分别为x1、x2.(1)求k的取值范围.
(2)若x1、x2满足x1x2-(x1+x2)=3,求k的值.
分析 (1)根据判别式的意义得到△=4(k-2)2-4(k2+4)=-16k≥0,然后解不等式即可;
(2)根据根与系数的关系得到得x1+x2=-2(k-2)=-2k+4,x1x2=k2+4,将两根之和和两根之积代入代数式求k的值即可.
解答 解:(1)∵一元二次方程x2+2(k-2)x+k2+4=0有两个实数根,
∴△=4(k-2)2-4(k2+4)=-16k≥0,
∴k≤0;
(2)∵一元二次方程x2+2(k-2)x+k2+4=0的两个根分别为x1、x2,
∴x1+x2=-2(k-2)=-2k+4,x1x2=k2+4,
∴x1x2-(x1+x2)=k2+4-(-2k+4)=k2+2k=3,
解得:k1=-3,k2=1,
∵k≤0,
∴k=-3.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程没有实数根.

练习册系列答案
相关题目
16.将△ABC的三个顶点的横坐标加上-3,纵坐标不变,则所得图( )
| A. | 向y轴的正方向平移了三个单位 | B. | 向x轴的正方向平移了三个单位 | ||
| C. | 向y轴的负方向平移了三个单位 | D. | 向x轴的负方向平移了三个单位 |
3.用换元法解方程(x2+x)(x2+x-1)=6,如果设x2+x=y,则原方程可变形为( )
| A. | y2+y-6=0 | B. | y2-y-6=0 | C. | y2-y+6=0 | D. | y2-y-6=0 |
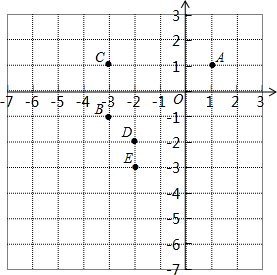 在同一平面直角坐标系中有6个点:
在同一平面直角坐标系中有6个点: 如图,已知AB=8,P是线段AB上的动点(不与A,B重合),以AP为边作正方形APMN,以PB为底作等腰△PBE(正方形APMN与△PBE在AB的同侧),连接ME,则△PME的面积的最大值为( )
如图,已知AB=8,P是线段AB上的动点(不与A,B重合),以AP为边作正方形APMN,以PB为底作等腰△PBE(正方形APMN与△PBE在AB的同侧),连接ME,则△PME的面积的最大值为( )