题目内容
16. 已知:如图,菱形ABCD的两条对角线相交于O,若AC=8,BD=6,则菱形ABCD的周长是( )
已知:如图,菱形ABCD的两条对角线相交于O,若AC=8,BD=6,则菱形ABCD的周长是( )| A. | 20 | B. | 16 | C. | 12 | D. | 10 |
分析 根据菱形的性质得AC⊥BD,OA=OC=4,OB=OD=3,AB=BC=CD=AD,再利用勾股定理计算出AB=5,然后计算菱形的周长.
解答 解:∵四边形ABCD为菱形,
∴AC⊥BD,OA=OC=4,OB=OD=3,AB=BC=CD=AD,
在Rt△OAB中,AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴菱形ABCD的周长=4AB=20.
故选A.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.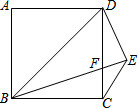 如图,在正方形ABCD中,BD=BE,CE∥BD,BE交CD于F点,则∠DFE的度数为( )
如图,在正方形ABCD中,BD=BE,CE∥BD,BE交CD于F点,则∠DFE的度数为( )
 如图,在正方形ABCD中,BD=BE,CE∥BD,BE交CD于F点,则∠DFE的度数为( )
如图,在正方形ABCD中,BD=BE,CE∥BD,BE交CD于F点,则∠DFE的度数为( )| A. | 45° | B. | 60° | C. | 75° | D. | 90° |
5.下列运算正确的是( )
| A. | a3•a2=a6 | B. | (a3)2=a6 | C. | a3+a2=a6 | D. | a3-a2=a |
6.在一个不透明的口袋中装有大小相同的5个球,其中有3个白球,2个黑球.现每次取一个,无放回地抽取两次,则在第一次抽到白球的条件下,第二次抽到白球的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{10}$ |
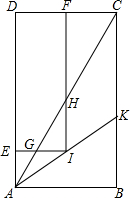 如图,已知矩形ABCD中,点I在∠CAB的平分线AK上运动,过I作IE⊥AD,IF⊥CD,垂足分别为E,F,IE、IF分别交AC于点G、H.
如图,已知矩形ABCD中,点I在∠CAB的平分线AK上运动,过I作IE⊥AD,IF⊥CD,垂足分别为E,F,IE、IF分别交AC于点G、H.