题目内容
20.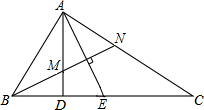 如图,AD是Rt△ABC斜边BC上的高,∠B的平分线交AD于点M,交AC于点N,∠DAC的平分线交CD于点E.求证:AE⊥MN,且AE平分MN.
如图,AD是Rt△ABC斜边BC上的高,∠B的平分线交AD于点M,交AC于点N,∠DAC的平分线交CD于点E.求证:AE⊥MN,且AE平分MN.
分析 由BE、AG分别是∠ABC、∠DAC的平分线.得到∠ABF=∠EBD.由于∠AFE=∠FAB+∠FBA,∠AEG=∠C+∠EBD,得到∠AFE=∠AEF,根据等腰三角形的性质可得结论.
解答 解:∵BE、AG分别是∠ABC、∠DAC的平分线.
∴∠ABF=∠EBD.
∵∠AFE=∠FAB+∠FBA,∠AEG=∠C+∠EBD,
∴∠AFE=∠AEF,
∴AF=AE,
∵∠DAC的平分线交CD于点E,
∴AE⊥MN,且AE平分MN.
点评 本题考查了等腰三角形的判定和性质,角平分线的性质,熟练掌握定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.下列说法中,错误的是( )
| A. | 若a>b,则a-b>0 | B. | 若a<b,则a-b<0 | ||
| C. | 若a=b,则a-b=0 | D. | 若a<0,b<0,则a-b<0 |
 如图,一张长方形纸条ABCD沿EF折叠,B′,C′分别是B,C的对应点,EB′平分∠AEF,求∠EFC′的度数.
如图,一张长方形纸条ABCD沿EF折叠,B′,C′分别是B,C的对应点,EB′平分∠AEF,求∠EFC′的度数.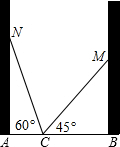 如图,在一个房间内,有一个梯子斜靠在墙上,梯子顶端距地面的垂直距离MB=m米,梯子的倾斜角度∠MCB=45°.若梯子斜靠在对面墙上,梯子的倾斜角度∠NCA=60°.试求该房间的宽和梯子的长度.
如图,在一个房间内,有一个梯子斜靠在墙上,梯子顶端距地面的垂直距离MB=m米,梯子的倾斜角度∠MCB=45°.若梯子斜靠在对面墙上,梯子的倾斜角度∠NCA=60°.试求该房间的宽和梯子的长度.