题目内容
15．
如图，一张长方形纸条ABCD沿EF折叠，B′，C′分别是B，C的对应点，EB′平分∠AEF，求∠EFC′的度数．
分析 如图，由折叠的性质可得∠FEB=∠B'EF，由角平分线的性质和邻补角可求得∠FEB．
解答 解：因为折叠的性质可得∠FEB=∠B'EF，
∵EB′平分∠AEF，
∴∠FEB=∠AEB'，
∵∠FEB+∠B'EF+∠AEB'=180°，
∴∠FEB=60°，
∴∠EFC′=120°．
点评 本题主要考查折叠的性质，掌握折叠的性质是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
3．在△ABC和△A′B′C′中，AB=A′B′，∠A=A′，∠C=∠C′，可知（1）∠B=∠B′；（2）∠B的平分线与∠B′的平分线相等；（3）BC边上的高与B′C′边上的高相等；（4）BC边上的中线与B′C′边上的中线相等，其中正确的结论有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
10．
实数a，b在数轴上对应的位置，如图所示：则|a-b|-|b|等于（ ）
实数a，b在数轴上对应的位置，如图所示：则|a-b|-|b|等于（ ）| A． | a | B． | a-2b | C． | -a | D． | b-a |
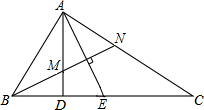如图，AD是Rt△ABC斜边BC上的高，∠B的平分线交AD于点M，交AC于点N，∠DAC的平分线交CD于点E．求证：AE⊥MN，且AE平分MN．