题目内容
11．△ABC中，AB=AC，AD⊥BC于D，若△ABC的周长为50，△ABD的周长为40，则AD=15．分析 由△ABC的周长为24得到AB，BC的关系，由△ABD的周长为20得到AB，BD，AD的关系，再由等腰三角形的性质知，BC为BD的2倍，故可解出AD的值．
解答 
解：∵△ABC的周长为50，AB=AC，
∴2AB+BC=50，
∵AD⊥BC，
∴BC=2BD，
∴2AB+2BD=50，
AB+BD=25，
∵△ABD的周长为40，
∴AB+BD+AD=40，
∴AD=15．
故答案为15．
点评 本题考查了等腰三角形的性质；由两个三角形的周长得到两个边之间的式子，通过整体代入求得AD的值是解答本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，方格纸中是4个相同的正方形，婉婷同学在这张方格纸上画了∠1、∠2、∠3三个角，那么∠1+∠2+∠3=135度．
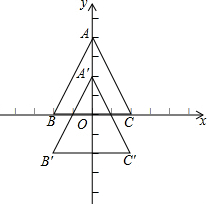如图所示，已知△ABC三个顶点的坐标分别是A（0，4），B（-2，0），C（3，0），把△ABC沿y轴向下平移2个单位得△A′B′C′
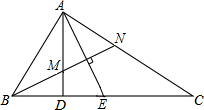如图，AD是Rt△ABC斜边BC上的高，∠B的平分线交AD于点M，交AC于点N，∠DAC的平分线交CD于点E．求证：AE⊥MN，且AE平分MN．