题目内容
12.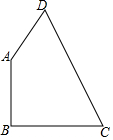 如图,在四边形ABCD中,已知AB=9cm,BC=12cm,AD=8cm,CD=17cm,且∠B=90°,求四边形ABCD的面积.
如图,在四边形ABCD中,已知AB=9cm,BC=12cm,AD=8cm,CD=17cm,且∠B=90°,求四边形ABCD的面积.
分析 连接AC,在Rt△ABC中,利用可勾股定理可得出AC,利用勾股定理的逆定理可判断△ADC是直角三角形,分别求出两个直角三角形的面积相加即可.
解答 解:连接AC,
在Rt△ABC中,AC=$\sqrt{A{C}^{2}+B{C}^{2}}$=15,
在△ADC中,AD=8cm,CD=17cm,
则AC2+AD2=DC2,
故可得△ADC为直角三角形,
四边形ABCD的面积=S△ABC+S△ADC=$\frac{1}{2}$AB×BC+$\frac{1}{2}$AD×AC=54+60=114.
点评 此题考查了勾股定理及勾股定理的逆定理,解答本题的关键是熟练掌握勾股定理的逆定理,判断出△ADC为直角三角形.

练习册系列答案
相关题目
2.为清理积压的库存,商场决定打折销售,已知甲、乙两种服装的原单价共为440元,现将甲服装打八折,乙服装打七五折,结果两种服装的单价共为342元,则甲、乙两种服装的原单价分别是( )
| A. | 200元,240元 | B. | 240元,200元 | C. | 280元,160元 | D. | 160元,280元 |
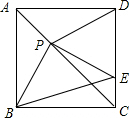 如图,正方形ABCD中,对角线AC上有一点P,连接BP、DP,过点P作PE⊥PB交CD于点E,连接BE.
如图,正方形ABCD中,对角线AC上有一点P,连接BP、DP,过点P作PE⊥PB交CD于点E,连接BE.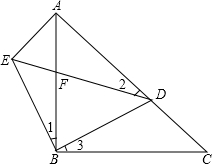 如图,三角形ABC,AB=BC,∠ABC=90°,∠1=∠2=∠3,
如图,三角形ABC,AB=BC,∠ABC=90°,∠1=∠2=∠3,