题目内容
20.设n是整数,请问(2n-1)2-1能否被8整除?若能,请加以证明;若不能,举出反例.分析 首先利用平方差公式对多项式(2n-1)2-1进行因式分解,得出原式=4n(n-1),再证明n(n-1)能被2整除,则(2n-1)2-1能被8整除.
解答 解:(2n-1)2-1能被8整除,理由如下:
(2n-1)2-1=(2n-1+1)(2n-1-1)=4n(n-1).
∵n是整数,
∴n与(n-1)是两个连续整数,n(n-1)能被2整除,
∴4n(n-1)能被8整除,即(2n-1)2-1能被8整除.
点评 此题主要考查了因式分解的应用,熟练掌握平方差公式是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

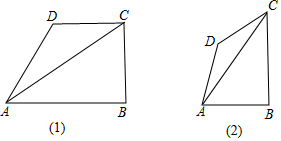
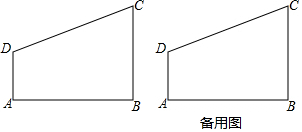 已知,直角梯形ABCD中,∠B=90°,AD=1,BC=2,AB=3,点M位于线段AB上,且△DMC是直角三角形,求线段AM的长度.
已知,直角梯形ABCD中,∠B=90°,AD=1,BC=2,AB=3,点M位于线段AB上,且△DMC是直角三角形,求线段AM的长度.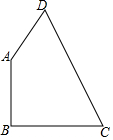 如图,在四边形ABCD中,已知AB=9cm,BC=12cm,AD=8cm,CD=17cm,且∠B=90°,求四边形ABCD的面积.
如图,在四边形ABCD中,已知AB=9cm,BC=12cm,AD=8cm,CD=17cm,且∠B=90°,求四边形ABCD的面积. 如图,在△ABC中,BD、CE分别是边AC、AB上的中线,BD与CE相交于点O,点M、N分别是OB、OC的中点.
如图,在△ABC中,BD、CE分别是边AC、AB上的中线,BD与CE相交于点O,点M、N分别是OB、OC的中点.