题目内容
7.若已知|x-1|+(2y+1)2+(3z+2)2=0,则2xy+z=$-1\frac{2}{3}$.分析 根据非负数的性质,可求出x、y的值,然后将代数式化简再代值计算.
解答 解:∵|x-1|+(2y+1)2+(3z+2)2=0,
∴x-1=0,2y+1=0,3z+2=0
∴x=1,y=-0.5,z=-$\frac{2}{3}$;
原式=$2×1×(-\frac{1}{2})-\frac{2}{3}=-1\frac{2}{3}$,
故答案为:$-1\frac{2}{3}$.
点评 本题考查了非负数的性质,一个数的绝对值加上一个数的平方为0,则这两个数都等于0.

练习册系列答案
相关题目
17. 某校为了解 八年级学生课外活动书籍借阅情况,从中随机抽取了50名学生课外书籍借阅情况.将统计结果列出如下的表格,并绘制如图所示的扇形统计图,其中科普类册数占这50名学生借阅总册数的40%.
某校为了解 八年级学生课外活动书籍借阅情况,从中随机抽取了50名学生课外书籍借阅情况.将统计结果列出如下的表格,并绘制如图所示的扇形统计图,其中科普类册数占这50名学生借阅总册数的40%.
(1)表格中字母m的值等于120;
(2)该校八年级共有400名学生,则可以估计出八年级学生共借阅教辅类书籍约880本.
 某校为了解 八年级学生课外活动书籍借阅情况,从中随机抽取了50名学生课外书籍借阅情况.将统计结果列出如下的表格,并绘制如图所示的扇形统计图,其中科普类册数占这50名学生借阅总册数的40%.
某校为了解 八年级学生课外活动书籍借阅情况,从中随机抽取了50名学生课外书籍借阅情况.将统计结果列出如下的表格,并绘制如图所示的扇形统计图,其中科普类册数占这50名学生借阅总册数的40%.| 类别 | 科普类 | 教辅类 | 文艺类 | 其他 |
| 册数(本) | 180 | 110 | m | 40 |
(2)该校八年级共有400名学生,则可以估计出八年级学生共借阅教辅类书籍约880本.
15.若分式$\frac{{x}^{2}-1}{x-1}$的值为0,则x的值为( )
| A. | 0 | B. | ±1 | C. | 1 | D. | -1 |
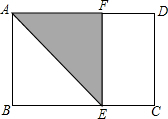 将长为1,宽为a的矩形纸片ABCD($\frac{1}{2}$<a<1)按如图方式折叠,剪下一个边长等于矩形宽度的正方形ABEF.若剩下的矩形EFDC与矩形ABCD相似,则a=$\frac{1+\sqrt{5}}{2}$.
将长为1,宽为a的矩形纸片ABCD($\frac{1}{2}$<a<1)按如图方式折叠,剪下一个边长等于矩形宽度的正方形ABEF.若剩下的矩形EFDC与矩形ABCD相似,则a=$\frac{1+\sqrt{5}}{2}$. 如图,在平面直角坐标系中,抛物线与x轴交于点A(-1,0)和点B(1,0),直线y=2x-1与y轴交于点C,与抛物线交于点C、D.求:
如图,在平面直角坐标系中,抛物线与x轴交于点A(-1,0)和点B(1,0),直线y=2x-1与y轴交于点C,与抛物线交于点C、D.求: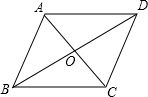 如图,平行四边形ABCD的对角线相交于O点,BC=14cm,BD=20cm,AC=12cm,则△AOD的周长为30cm.
如图,平行四边形ABCD的对角线相交于O点,BC=14cm,BD=20cm,AC=12cm,则△AOD的周长为30cm.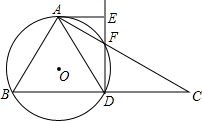 如图,在Rt△ABC中,斜边BC=12,∠C=30°,D为BC的中点,△ABD的外接圆⊙O与AC交于F点,过A作⊙O的切线AE交DF的延长线于E点.
如图,在Rt△ABC中,斜边BC=12,∠C=30°,D为BC的中点,△ABD的外接圆⊙O与AC交于F点,过A作⊙O的切线AE交DF的延长线于E点.