题目内容
三角形三条边长分别为1、2、
,求其三条中线长.
| 3 |
考点:勾股定理的逆定理,直角三角形的性质,勾股定理
专题:
分析:先根据勾股定理的逆定理判定△ABC为直角三角形,再利用勾股定理求出中线AD与BE的长,利用直角三角形的性质求得斜边上的中线CF的长.
解答: 解:如图,△ABC中,AC=1,BC=
解:如图,△ABC中,AC=1,BC=
,AB=2,
∵12+(
)2=22,
∴△ABC为直角三角形,∠ACB=90°,
∴斜边长AB为2,
∵直角三角形中斜边上的中线等于斜边的一半,
∴CF=
AB=1.
在Rt△ACD中,∵∠ACD=90°,
∴AD=
=
=
.
Rt△BCE中,∵∠BCE=90°,
∴BE=
=
=
.
 解:如图,△ABC中,AC=1,BC=
解:如图,△ABC中,AC=1,BC=| 3 |
∵12+(
| 3 |
∴△ABC为直角三角形,∠ACB=90°,
∴斜边长AB为2,
∵直角三角形中斜边上的中线等于斜边的一半,
∴CF=
| 1 |
| 2 |
在Rt△ACD中,∵∠ACD=90°,
∴AD=
| AC2+CD2 |
12+(
|
| ||
| 2 |
Rt△BCE中,∵∠BCE=90°,
∴BE=
| BC2+CE2 |
(
|
| ||
| 2 |
点评:本题考查了勾股定理的逆定理,勾股定理,还利用了直角三角形中斜边上的中线等于斜边的一半的性质.利用勾股定理的逆定理判定△ABC为直角三角形是解题的关键.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
下列图形中,一定是轴对称图形的有( )个.
①角;②圆;③等腰三角形;④等边三角形;⑤直角三角形.
①角;②圆;③等腰三角形;④等边三角形;⑤直角三角形.
| A、1个 | B、2个 | C、3个 | D、4个 |
 甲、乙两人从顺义少年宫出发,沿相同的线路跑向顺义公园,甲先跑一段路程后,乙开始出发,当乙超过甲150米时,乙停在此地等候甲,两人相遇后,乙和甲一起以甲原来的速度跑向顺义公园,如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象,请根据题意解答下列问题.
甲、乙两人从顺义少年宫出发,沿相同的线路跑向顺义公园,甲先跑一段路程后,乙开始出发,当乙超过甲150米时,乙停在此地等候甲,两人相遇后,乙和甲一起以甲原来的速度跑向顺义公园,如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象,请根据题意解答下列问题.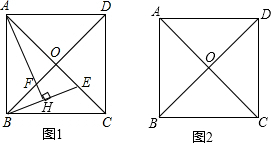 如图,已知正方形ABCD,AC、BD相交于点O,E为AC上一点,AH⊥EB交EB于点H,AH交BD于点F.
如图,已知正方形ABCD,AC、BD相交于点O,E为AC上一点,AH⊥EB交EB于点H,AH交BD于点F. 如图所示,直线AB与反比例函数图象相交于A、B两点,已知A(1,4),连接OA、OB,当△AOB的面积为
如图所示,直线AB与反比例函数图象相交于A、B两点,已知A(1,4),连接OA、OB,当△AOB的面积为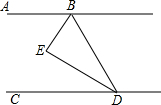 如图,已知,BE平分∠ABD,DE平分∠BDC,且∠EBD+∠EDB=90°.
如图,已知,BE平分∠ABD,DE平分∠BDC,且∠EBD+∠EDB=90°. 为了改善小区环境,某小区决定在一块一边靠墙(墙长为25m)的空地上修建一个长方形绿化带ABCD.绿化带一面靠墙,另外三面用总长为40m的栅栏围住.
为了改善小区环境,某小区决定在一块一边靠墙(墙长为25m)的空地上修建一个长方形绿化带ABCD.绿化带一面靠墙,另外三面用总长为40m的栅栏围住. 如图,?ABCD中,E,F分别是AD,BC的中点,当AB与AC满足条件
如图,?ABCD中,E,F分别是AD,BC的中点,当AB与AC满足条件