题目内容
15. 如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.(1)边AC的长等于5.
(2)以点C为旋转中心,把△ABC顺时针旋转,得到△A′B′C,使点B的对应点B′恰好落在边AC上,请在如图所示的网格中,用无刻度的直尺,作出旋转后的图形,并简要说明画图方法(不要求证明).
分析 (1)根据勾股定理即可解决问题.
(2)利用格点构造全等三角形,使得CB′=FH=3,EF⊥AC,A′B′=4即可解决问题.
解答 解:(1)AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5.
故答案为5;
(2)如图,取格点E、F、M、N,作直线EF、直线MN,MN与EF交于点A′,EF与AC交于点B′,连接CA′,则△CA′B′即为所求.
点评 本题考查作图-旋转变换,解题的关键是利用格点构造全等三角形,使得CB′=FH=3,EF⊥AC,A′B′=4,题目比较难,是作图题目中比较难的题目.

练习册系列答案
相关题目
5.下列各式中计算正确的是( )
| A. | (-a2)5=-a10 | B. | (x4)3=x7 | C. | b5•b5=b25 | D. | a6÷a2=a3 |
6.下列计算正确的是( )
| A. | (x+2)(x-2)=x2-2 | B. | (a+b)(b-a)=a2-b2 | C. | (-a+b)2=a2-2ab+b2 | D. | (-a-b)2=a2-2ab+b2 |
3.下列方程中,是二元一次方程的是( )
| A. | 3x-2y=4z | B. | 6xy+9=0 | C. | 4x=$\frac{y-2}{4}$ | D. | $\frac{1}{x}$+4y=6 |
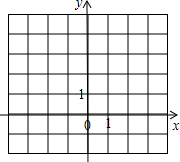 在如图所示的坐标系中,己知A(-3,4),B(-2,1),C(-1,3).
在如图所示的坐标系中,己知A(-3,4),B(-2,1),C(-1,3).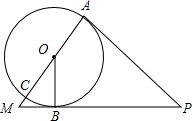 如图,AC是⊙O的直径,PA切⊙O于点A,点B在⊙O上,PA=PB,PB的延长线与AC的延长线交于点M.
如图,AC是⊙O的直径,PA切⊙O于点A,点B在⊙O上,PA=PB,PB的延长线与AC的延长线交于点M.