题目内容
20．已知二次函数y=a（x-2）2+c，当x=x1时，函数值为y1；当x=x2时，函数值为y2，若|x1-2|＞|x2-2|，则下列表达式正确的是（ ）| A． | y1+y2＞0 | B． | y1-y2＞0 | C． | a（y1-y2）＞0 | D． | a（y1+y2）＞0 |
分析 分a＞0和a＜0两种情况根据二次函数的对称性确定出y1与y2的大小关系，然后对各选项分析判断即可得解．
解答 解：①a＞0时，二次函数图象开口向上，
∵|x1-2|＞|x2-2|，
∴y1＞y2，
无法确定y1+y2的正负情况，
a（y1-y2）＞0，
②a＜0时，二次函数图象开口向下，
∵|x1-2|＞|x2-2|，
∴y1＜y2，
无法确定y1+y2的正负情况，
a（y1-y2）＞0，
综上所述，表达式正确的是a（y1-y2）＞0．
故选C．
点评 本题考查了二次函数图象上点的坐标特征，主要利用了二次函数的对称性，难点在于根据二次项系数a的正负情况分情况讨论．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
8．
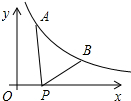如图所示，已知A（0.2，y1），B（2，y2）为反比例函数y=$\frac{1}{x}$ 图象上的两点，动点P（x，0）在x轴正半轴上运动，当线段AP与线段BP之差达到最大时，点P的坐标是（ ）
如图所示，已知A（0.2，y1），B（2，y2）为反比例函数y=$\frac{1}{x}$ 图象上的两点，动点P（x，0）在x轴正半轴上运动，当线段AP与线段BP之差达到最大时，点P的坐标是（ ）| A． | （0.5，0） | B． | （1，0） | C． | （1.5，0） | D． | （2.5，0） |
已知，正六边形ABCDEF在直角坐标系内的位置如图所示，A（-2，0），点B在原点，把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转，每次翻转60°，经过2015次翻转之后，点B的坐标是（4031，$\sqrt{3}$）．
13．若关于x的一元二次方程x2+ax+b=0有两个不同的实数根m，n（m＜n），方程x2+ax+b=2有两个不同的实数根p，q（p＜q），则m，n，p，q的大小关系为（ ）
| A． | p＜m＜n＜q | B． | m＜p＜q＜n | C． | m＜p＜n＜q | D． | p＜m＜q＜n |