题目内容
19.将二次函数y=x2-1的图象向右平移一个单位长度,再向上平移3个单位长度所得的抛物线的解析式为( )| A. | y=(x-1)2+2 | B. | y=(x+1)2+2 | C. | y=(x-1)2-2 | D. | y=(x+1)2-2 |
分析 先确定二次函数y=x2-1的顶点坐标为(0,-1),再把点(0,-1)向右平移一个单位长度,再向上平移3个单位长度得到点的坐标为(1,2),然后根据抛物线的顶点式写出平移后的抛物线解析式.
解答 解:二次函数y=x2-1的顶点坐标为(0,-1),把点(0,-1)向右平移一个单位长度,再向上平移3个单位长度得到点的坐标为(1,2),所以所得的图象解析式为
y=(x-1)2+2.
故选:A.
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.已知三角形两边长分别为3和8,则该三角形第三边的长可能是( )
| A. | 3 | B. | 5 | C. | 8 | D. | 11 |
8.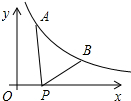 如图所示,已知A(0.2,y1),B(2,y2)为反比例函数y=$\frac{1}{x}$ 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
如图所示,已知A(0.2,y1),B(2,y2)为反比例函数y=$\frac{1}{x}$ 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
 如图所示,已知A(0.2,y1),B(2,y2)为反比例函数y=$\frac{1}{x}$ 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
如图所示,已知A(0.2,y1),B(2,y2)为反比例函数y=$\frac{1}{x}$ 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )| A. | (0.5,0) | B. | (1,0) | C. | (1.5,0) | D. | (2.5,0) |
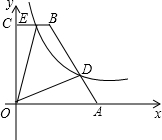 如图,在直角梯形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0),(2,6),点D为AB上一点,且BD=2AD,函数y=$\frac{k}{x}$(k>0)经过点D,交BC于点E.
如图,在直角梯形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0),(2,6),点D为AB上一点,且BD=2AD,函数y=$\frac{k}{x}$(k>0)经过点D,交BC于点E.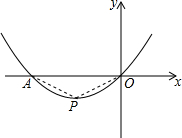 已知抛物线y=ax2+bx+c(a≠0)的图象经过原点O,交x轴于点A,其顶点P的坐标为(-$\sqrt{3}$,-1)
已知抛物线y=ax2+bx+c(a≠0)的图象经过原点O,交x轴于点A,其顶点P的坐标为(-$\sqrt{3}$,-1)